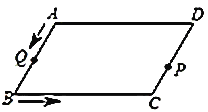
【题目】如图,平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 与点
与点![]() 是平行四边形
是平行四边形![]() 边上的动点,点
边上的动点,点![]() 以每秒
以每秒![]() 个单位长度的速度,从点
个单位长度的速度,从点![]() 运动到点
运动到点![]() ,点
,点![]() 以每秒
以每秒![]() 个单位长度的速度从点
个单位长度的速度从点![]() →点
→点![]() →点
→点![]() 运动.当其中一个点到达终点时,另一个随之停止运动.点
运动.当其中一个点到达终点时,另一个随之停止运动.点![]() 与点
与点![]() 同时出发,设运动时间为
同时出发,设运动时间为![]() ,
,![]() 的面积为
的面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)![]() 为何值时,将
为何值时,将![]() 以它的一边为轴翻折,翻折前后的两个三角形所组成的四边形为菱形.
以它的一边为轴翻折,翻折前后的两个三角形所组成的四边形为菱形.
参考答案:
【答案】(1)①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时,![]() ;(2)
;(2)![]() 时,
时,![]() 不是等腰三角形,所以不存在符合条件的菱形. 当
不是等腰三角形,所以不存在符合条件的菱形. 当![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.
【解析】
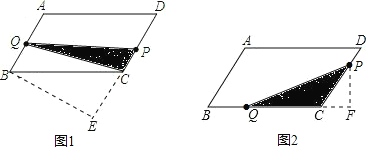
(1)当0<t≤2时,如图1,过点B作BE⊥CD,交DC的延长线于点E,根据三角形面积公式求得S关于t的函数关系式,当2<t≤4时,如图2,CP=t,BQ=2t-4,过点P作PF⊥BC,交BC的延长线于F点,由三角形面积公式求得S关于t的函数关系式,
(2)要使翻折前后的两个三角形所组成的四边形为菱形,则△CPQ为等腰三角形,则要CQ=CP,看看t是否存在.
(1)①当![]() 时,如图1,过点
时,如图1,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,
,
∴∠BED=90°,即∠BCE+∠CBE=90°,
∵四边形![]() 是平行四边形,∴AD∥BC,
是平行四边形,∴AD∥BC,
![]()
![]() ,
,![]()
![]()
![]() ,由勾股定理得:
,由勾股定理得:![]() ,
,
∵![]() ,
,
∴![]() ;
;
②当![]() 时,由题意得:CP=t,
时,由题意得:CP=t,![]() ,
,![]() ,
,
如图2,过点P作PF⊥BC,交BC的延长线于点F,
∴∠F=90°,
∵四边形![]() 是平行四边形,∴AB∥DC,
是平行四边形,∴AB∥DC,
∴![]() ,∵
,∵![]() ,
,
![]()
![]() ,
,
![]()
![]() ,由勾股定理得:
,由勾股定理得:![]() ,
,
∴![]() ,
,
即![]() .
.
∴S=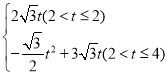 .
.
(2)当![]() 时,
时,![]() 不是等腰三角形,所以不存在符合条件的菱形.
不是等腰三角形,所以不存在符合条件的菱形.
当![]() 时,令
时,令![]() ,即
,即![]() ,解得
,解得![]()
![]() 当
当![]() 时,
时,![]() 为等腰三角形,
为等腰三角形,
即为![]() 的一边所在直线为轴翻折,翻折前后的两个三角形组成的四边形为菱形.
的一边所在直线为轴翻折,翻折前后的两个三角形组成的四边形为菱形.
-
科目: 来源: 题型:
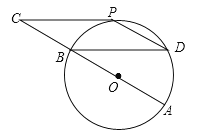
查看答案和解析>>【题目】如图,⊙O的直径AB=12cm,C为AB延长线上一点,CP与⊙O相切于点P,过点B作弦BD∥CP,连接PD.
(1)求证:点P为
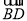 的中点;
的中点;(2)若∠C=∠D,求四边形BCPD的面积.
-
科目: 来源: 题型:
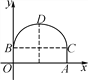
查看答案和解析>>【题目】如图,东湖隧道的截面由抛物线和长方形构成,长方形的长OA为12 m,宽OB为4 m,隧道顶端D到路面的距离为10 m,建立如图所示的直角坐标系.
(1)求该抛物线的表达式;
(2)一辆货车载有一个长方体集装箱,集装箱最高处与地面距离为6 m,宽为4 m,隧道内设双向行车道,问这辆货车能否安全通过?
(3)在抛物线形拱壁上需要安装两排离地面高度相等的灯,如果灯离地面的高度不超过8.5 m,那么这两排灯的水平距离最小是多少米?
-
科目: 来源: 题型:
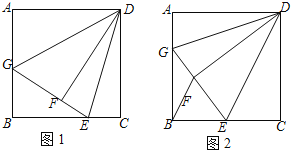
查看答案和解析>>【题目】如图1,在正方形
 中,点
中,点 为
为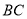 上一点,连接
上一点,连接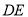 ,把
,把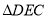 沿
沿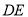 折叠得到
折叠得到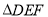 ,延长
,延长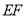 交
交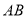 于
于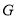 ,连接
,连接 .
.
(1)求
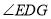 的度数.
的度数.(2)如图
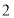 ,
,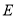 为
为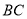 的中点,连接
的中点,连接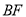 .
.①求证:
 ;
; ②若正方形边长为
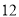 ,求线段
,求线段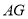 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】通过学习绝对值,我们知道
 的几何意义是数轴上表示数
的几何意义是数轴上表示数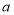 在数轴上的对应点与原点的距离,如:
在数轴上的对应点与原点的距离,如: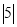 表示
表示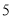 在数轴上的对应点到原点的距离.
在数轴上的对应点到原点的距离.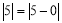 ,即
,即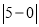 表示
表示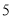 、
、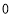 在数轴上对应的两点之间的距离,类似的,
在数轴上对应的两点之间的距离,类似的,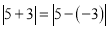 ,即
,即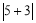 表示
表示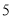 、
、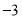 在数轴上对应的两点之间的距离;一般地,点
在数轴上对应的两点之间的距离;一般地,点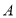 ,
,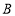 在数轴上分别表示数
在数轴上分别表示数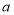 、
、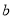 ,那么
,那么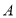 ,
,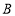 之间的距离可表示为
之间的距离可表示为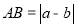 .
.请根据绝对值的几何意义并结合数轴解答下列问题:
(1)数轴上表示
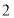 和
和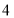 的两点之间的距离是___;数轴上
的两点之间的距离是___;数轴上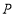 、
、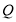 两点的距离为
两点的距离为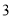 ,点
,点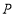 表示的数是
表示的数是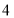 ,则点
,则点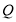 表示的数是___.
表示的数是___.(2)点
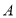 ,
,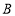 ,
,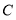 在数轴上分别表示数
在数轴上分别表示数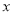 、
、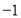 、
、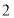 ,那么
,那么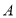 到点
到点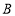 .点
.点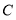 的距离之和可表示为_ (用含绝对值的式子表示);若
的距离之和可表示为_ (用含绝对值的式子表示);若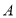 到点
到点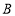 .点
.点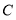 的距离之和有最小值,则
的距离之和有最小值,则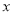 的取值范围是_ __.
的取值范围是_ __.(3)
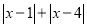 的最小值为_ __.
的最小值为_ __. -
科目: 来源: 题型:
查看答案和解析>>【题目】同学们都知道,
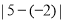 表示5与
表示5与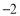 之差的绝对值,实际上也可以理解为5与
之差的绝对值,实际上也可以理解为5与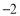 两数在数轴上所对应的两点之间的距离.回答下列问题:
两数在数轴上所对应的两点之间的距离.回答下列问题:(1)
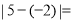 _______.
_______.(2)找出所有符合条件的整数
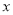 ,使得
,使得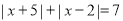 成立,这样的整数是______.
成立,这样的整数是______.(3)对于任何有理数
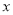 ,
,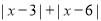 的最小值是______.
的最小值是______.(4)对于任何有理数
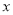 ,
,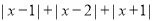 的最小值是_____,此时
的最小值是_____,此时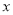 的值是______.
的值是______. -
科目: 来源: 题型:
查看答案和解析>>【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在四边形ABCD中,BC=AD,AB=

求证:四边形ABCD是 四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇同学的思路写出证明过程;
(3)用文字叙述所证命题的逆命题.
相关试题

