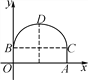
【题目】如图,东湖隧道的截面由抛物线和长方形构成,长方形的长OA为12 m,宽OB为4 m,隧道顶端D到路面的距离为10 m,建立如图所示的直角坐标系.
(1)求该抛物线的表达式;
(2)一辆货车载有一个长方体集装箱,集装箱最高处与地面距离为6 m,宽为4 m,隧道内设双向行车道,问这辆货车能否安全通过?
(3)在抛物线形拱壁上需要安装两排离地面高度相等的灯,如果灯离地面的高度不超过8.5 m,那么这两排灯的水平距离最小是多少米?
参考答案:
【答案】(1) y=-![]() (x-6)2+10(2)这辆货车能安全通过(3)两排灯的水平距离最小是6 m.
(x-6)2+10(2)这辆货车能安全通过(3)两排灯的水平距离最小是6 m.
【解析】试题分析:(1)设出抛物线的解析式,根据抛物线顶点坐标,代入解析式;
(2)令x=10,求出y与6作比较;
(3)求出y=8.5时x的值即可得.
试题解析:(1)根据题意,该抛物线的顶点坐标为(6,10),设抛物线的表达式为
y=a(x-6)2+10,将点B(0,4)代入,得36a+10=4,解得a=-![]() .
.
故该抛物线的表达式为y=-![]() (x-6)2+10.
(x-6)2+10.
(2)根据题意,当x=6+4=10时,y=-![]() ×16+10=
×16+10=![]() >6,∴这辆货车能安全通过.
>6,∴这辆货车能安全通过.
(3)当y=8.5时,有-![]() (x-6)2+10=8.5,解得x1=3,x2=9,∴x2-x1=6.
(x-6)2+10=8.5,解得x1=3,x2=9,∴x2-x1=6.
答:两排灯的水平距离最小是6 m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一座弧形的拱桥,桥下水面的宽度AB为7.2米,拱顶高出水面CD的长为2.4米,现有一艘宽3米,船舱顶部为长方形并且高出水面2米的货船要经过这里,此货船能顺利通过这座弧形拱桥吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明元旦节吃完晚饭后6点过还没到7点,他陪他妈到成华区SM广场去买东西,离家时他发现他家的时钟上时针与分针刚好重合,他离家的时间是_______(用几点几分几秒表示,注意“四舍五入”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径AB=12cm,C为AB延长线上一点,CP与⊙O相切于点P,过点B作弦BD∥CP,连接PD.
(1)求证:点P为
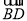 的中点;
的中点;(2)若∠C=∠D,求四边形BCPD的面积.
-
科目: 来源: 题型:
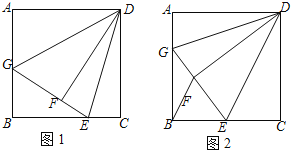
查看答案和解析>>【题目】如图1,在正方形
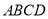 中,点
中,点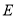 为
为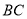 上一点,连接
上一点,连接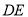 ,把
,把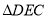 沿
沿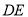 折叠得到
折叠得到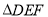 ,延长
,延长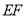 交
交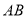 于
于 ,连接
,连接 .
.
(1)求
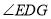 的度数.
的度数.(2)如图
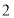 ,
,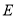 为
为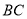 的中点,连接
的中点,连接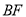 .
.①求证:
 ;
; ②若正方形边长为
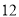 ,求线段
,求线段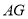 的长.
的长. -
科目: 来源: 题型:
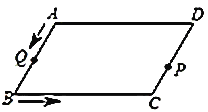
查看答案和解析>>【题目】如图,平行四边形
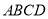 中,
中,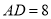 ,
,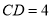 ,
,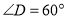 ,点
,点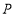 与点
与点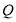 是平行四边形
是平行四边形 边上的动点,点
边上的动点,点 以每秒
以每秒 个单位长度的速度,从点
个单位长度的速度,从点 运动到点
运动到点 ,点
,点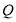 以每秒
以每秒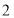 个单位长度的速度从点
个单位长度的速度从点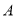 →点
→点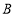 →点
→点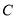 运动.当其中一个点到达终点时,另一个随之停止运动.点
运动.当其中一个点到达终点时,另一个随之停止运动.点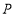 与点
与点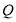 同时出发,设运动时间为
同时出发,设运动时间为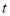 ,
,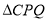 的面积为
的面积为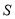 .
.
(1)求
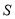 关于
关于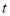 的函数关系式;
的函数关系式; (2)
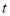 为何值时,将
为何值时,将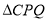 以它的一边为轴翻折,翻折前后的两个三角形所组成的四边形为菱形.
以它的一边为轴翻折,翻折前后的两个三角形所组成的四边形为菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】通过学习绝对值,我们知道
 的几何意义是数轴上表示数
的几何意义是数轴上表示数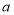 在数轴上的对应点与原点的距离,如:
在数轴上的对应点与原点的距离,如: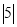 表示
表示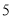 在数轴上的对应点到原点的距离.
在数轴上的对应点到原点的距离.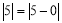 ,即
,即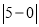 表示
表示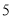 、
、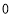 在数轴上对应的两点之间的距离,类似的,
在数轴上对应的两点之间的距离,类似的,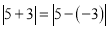 ,即
,即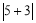 表示
表示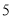 、
、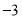 在数轴上对应的两点之间的距离;一般地,点
在数轴上对应的两点之间的距离;一般地,点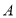 ,
,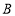 在数轴上分别表示数
在数轴上分别表示数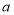 、
、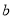 ,那么
,那么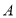 ,
,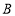 之间的距离可表示为
之间的距离可表示为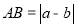 .
.请根据绝对值的几何意义并结合数轴解答下列问题:
(1)数轴上表示
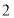 和
和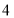 的两点之间的距离是___;数轴上
的两点之间的距离是___;数轴上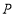 、
、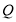 两点的距离为
两点的距离为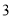 ,点
,点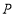 表示的数是
表示的数是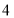 ,则点
,则点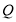 表示的数是___.
表示的数是___.(2)点
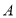 ,
,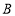 ,
,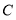 在数轴上分别表示数
在数轴上分别表示数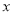 、
、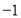 、
、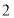 ,那么
,那么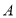 到点
到点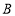 .点
.点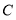 的距离之和可表示为_ (用含绝对值的式子表示);若
的距离之和可表示为_ (用含绝对值的式子表示);若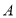 到点
到点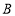 .点
.点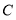 的距离之和有最小值,则
的距离之和有最小值,则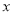 的取值范围是_ __.
的取值范围是_ __.(3)
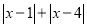 的最小值为_ __.
的最小值为_ __.
相关试题

