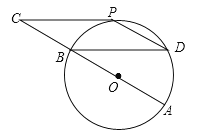
【题目】如图,⊙O的直径AB=12cm,C为AB延长线上一点,CP与⊙O相切于点P,过点B作弦BD∥CP,连接PD.
(1)求证:点P为![]() 的中点;
的中点;
(2)若∠C=∠D,求四边形BCPD的面积.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
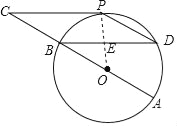
【解析】试题分析:(1)连接OP,根据切线的性质得到PC⊥OP,根据平行线的性质得到BD⊥OP,根据垂径定理即可得到结论;
(2)根据圆周角定理得到∠POB=2∠D,根据三角形的内角和得到∠C=30°,推出四边形BCPD是平行四边形,于是得到结论.
试题解析:(1)连接OP,
∵CP与⊙O相切于点P,
∴PC⊥OP,
∵BD∥CP,
∴BD⊥OP,
∴![]() ,
,
∴点P为![]() 的中点;
的中点;
(2)∵∠C=∠D,
∵∠POB=2∠D,
∴∠POB=2∠C,
∵∠CPO=90°,
∴∠C=30°,
∵BD∥CP,
∴∠C=∠DBA,
∴∠D=∠DBA,
∴BC∥PD,
∴四边形BCPD是平行四边形,
∵PO=![]() AB=6,
AB=6,
∴PC=6![]() ,
,
∵∠ABD=∠C=30°,
∴OE=![]() OB=3,
OB=3,
∴PE=3,
∴四边形BCPD的面积=PCPE=6![]() ×3=18
×3=18![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)如图①,若点E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图②,若∠EAF=60°,求证:△AEF是等边三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有一座弧形的拱桥,桥下水面的宽度AB为7.2米,拱顶高出水面CD的长为2.4米,现有一艘宽3米,船舱顶部为长方形并且高出水面2米的货船要经过这里,此货船能顺利通过这座弧形拱桥吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明元旦节吃完晚饭后6点过还没到7点,他陪他妈到成华区SM广场去买东西,离家时他发现他家的时钟上时针与分针刚好重合,他离家的时间是_______(用几点几分几秒表示,注意“四舍五入”).
-
科目: 来源: 题型:
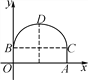
查看答案和解析>>【题目】如图,东湖隧道的截面由抛物线和长方形构成,长方形的长OA为12 m,宽OB为4 m,隧道顶端D到路面的距离为10 m,建立如图所示的直角坐标系.
(1)求该抛物线的表达式;
(2)一辆货车载有一个长方体集装箱,集装箱最高处与地面距离为6 m,宽为4 m,隧道内设双向行车道,问这辆货车能否安全通过?
(3)在抛物线形拱壁上需要安装两排离地面高度相等的灯,如果灯离地面的高度不超过8.5 m,那么这两排灯的水平距离最小是多少米?
-
科目: 来源: 题型:
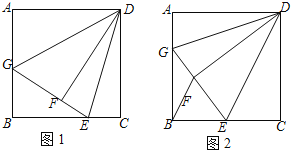
查看答案和解析>>【题目】如图1,在正方形
 中,点
中,点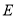 为
为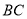 上一点,连接
上一点,连接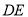 ,把
,把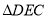 沿
沿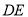 折叠得到
折叠得到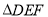 ,延长
,延长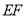 交
交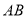 于
于 ,连接
,连接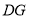 .
.
(1)求
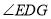 的度数.
的度数.(2)如图
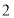 ,
,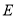 为
为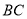 的中点,连接
的中点,连接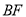 .
.①求证:
 ;
; ②若正方形边长为
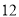 ,求线段
,求线段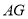 的长.
的长. -
科目: 来源: 题型:
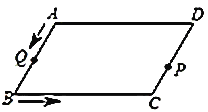
查看答案和解析>>【题目】如图,平行四边形
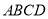 中,
中,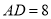 ,
,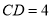 ,
,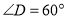 ,点
,点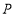 与点
与点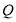 是平行四边形
是平行四边形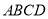 边上的动点,点
边上的动点,点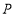 以每秒
以每秒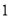 个单位长度的速度,从点
个单位长度的速度,从点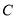 运动到点
运动到点 ,点
,点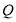 以每秒
以每秒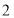 个单位长度的速度从点
个单位长度的速度从点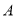 →点
→点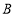 →点
→点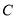 运动.当其中一个点到达终点时,另一个随之停止运动.点
运动.当其中一个点到达终点时,另一个随之停止运动.点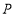 与点
与点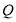 同时出发,设运动时间为
同时出发,设运动时间为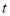 ,
,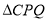 的面积为
的面积为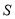 .
.
(1)求
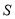 关于
关于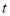 的函数关系式;
的函数关系式; (2)
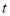 为何值时,将
为何值时,将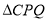 以它的一边为轴翻折,翻折前后的两个三角形所组成的四边形为菱形.
以它的一边为轴翻折,翻折前后的两个三角形所组成的四边形为菱形.
相关试题

