搜索
【题目】如图，等腰△ABC中，AB=AC，∠BAC=50°，AB的垂直平分线MN交AC于点D，则∠DBC的度数是 ．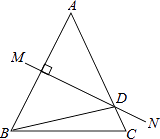 
参考答案：
【答案】15°
【解析】解：∵AB=AC，∠A=40°， ∴∠ABC= 
（180°﹣∠A）= （180°﹣50°）=65°，
∵MN垂直平分线AB，
∴AD=BD，
∴∠ABD=∠A=50°，
∴∠DBC=∠ABC﹣∠ABD=65°﹣50°=15°．
所以答案是：15°．
【考点精析】根据题目的已知条件，利用线段垂直平分线的性质和等腰三角形的性质的相关知识可以得到问题的答案，需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等；等腰三角形的两个底角相等（简称：等边对等角）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，点G为BC边的中点，点H在AF上，动点P以每秒1cm的速度沿图1的边运动，运动路径为
，相应的
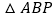的面积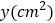
关于运动时间
的函数图象如图2，若
，则下列结论正确的个数有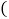
图1中BC长4cm；
图1中DE的长是3cm；
图2中点M表示4秒时的y值为
；
图2中的点N表示12秒时y值为
．
A. 1个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】“赵爽炫图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽炫图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为
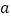,较短直角边长为
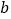，若(a+b)2=21，大正方形的面积为13，则小正方形的边长为( )
A.
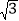B. 2 C. 
D.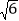 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过第2018次运动后，动点P的坐标是_____________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形网格中的△ABC，若小方格边长为1，格点△ABC（顶点是网格线交点的三角形）的顶点A，C的坐标分别为（﹣1，1），（0，﹣2），请你根据所学的知识．
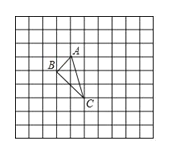
（1）在如图所示的网格平面内作出平面直角坐标系；
（2）作出△ABC关于y轴对称的三角形A1B1C1；
（3）判断△ABC的形状，并求出△ABC的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知直线y=kx+b经过点A（0，6），且平行于直线y=-2x.
（1）求该函数的解析式，并画出它的图象；
（2）如果这条直线经过点P（m，2），求m的值；
（3）若O为坐标原点，求直线OP的解析式；
（4）求直线y=kx+b和直线OP与坐标轴所围成的图形的面积.
-
科目： 来源： 题型：
查看答案和解析>>【题目】观察图形找出规律，并解答问题．
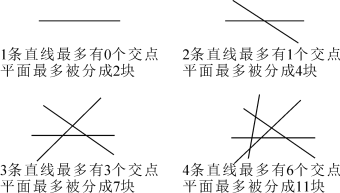
(1)5条直线相交，最多有_____个交点，平面最多被分成_____块；
(2)n条直线相交，最多有__________个交点，平面最多被分成____________块．
相关试题
