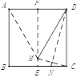
【题目】如图,先将正方形纸片对折,折痕为EF,再把点C折叠到EF上,折痕为DN,点C在EF上的对应点为M,则下列结论中(1)AM=AB;(2)∠MCE=15°;(3)△AMD是等边三角形;(4)CN=NE,正确的个数有( )
A. 1个B. 2个C. 3个D. 4个
参考答案:
【答案】C
【解析】
根据翻折变换的性质、正方形的性质,结合题意即可判断,得出答案.
(1)根据翻折变换的性质可知DM=DC,由将正方形纸片对折,折痕为EF,可知AM=DM,根据正方形的性质可知DC=AB,所以AM=AB,(1)正确;∵四边形ABCD是正方形,∴AD=CD,∠ADC=90°, ∵将正方形纸片ABCD对折,折痕为EF,∴AM=DM,∵把点C折叠在EF上,折痕为DN,∴DM=DC,∴AD=DM=AM,∴△ADM是等边三角形,∴∠ADM=60°,∴∠MDC=30°,∴∠DMC=75°,∴∠CME=180°-30°-75°=75°,则∠MCE=90°-75°=15°.所以(2)正确;由(1)可知AM=DM,DM=DC,根据正方形的性质可知AD=DM,所以△AMD是等边三角形,(3)正确;根据已知条件不能得出CN=NE ,所以(4)错误;故答案选择C项.
-
科目: 来源: 题型:
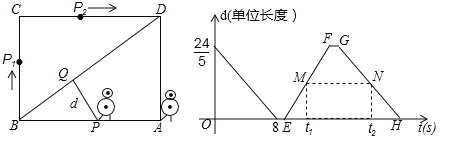
查看答案和解析>>【题目】(2017江苏省苏州市)某校机器人兴趣小组在如图①所示的矩形场地上开展训练.机器人从点A出发,在矩形ABCD边上沿着A→B→C→D的方向匀速移动,到达点D时停止移动.已知机器人的速度为1个单位长度/s,移动至拐角处调整方向需要1s(即在B、C处拐弯时分别用时1s).设机器人所用时间为t(s)时,其所在位置用点P表示,P到对角线BD的距离(即垂线段 PQ的长)为d个单位长度,其中d与t的函数图象如图②所示.
(1)求AB、BC的长;
(2)如图②,点M、N分别在线段EF、GH上,线段MN平行于横轴,M、N的横坐标分别为t1、t2.设机器人用了t1(s)到达点P1处,用了t2(s)到达点P2处(见图①).若CP1+CP2=7,求t1、t2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校计划购买若干台电脑,现从两家商场了解到同一型号电脑每台报价均为4000元,并且多买都有一定的优惠.甲商场的优惠条件是:第一台按原价收费,其余每台优惠25%;乙商场的优惠条件是:每台优惠20%.
(1)设该学校所买的电脑台数是x台,选择甲商场时,所需费用为
 元,选择乙商场时,所需费用为
元,选择乙商场时,所需费用为 元,请分别写出
元,请分别写出 ,
,  与x之间的关系式;
与x之间的关系式;(2)该学校如何根据所买电脑的台数选择到哪间商场购买,所需费用较少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.

-
科目: 来源: 题型:
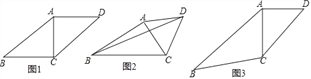
查看答案和解析>>【题目】已知△ABC,以AC为边在△ABC外作等腰△ACD,其中AC=AD.
(1)如图1,若∠DAC=2∠ABC,AC=BC,四边形ABCD是平行四边形,则∠ABC= ;
(2)如图2,若∠ABC=30°,△ACD是等边三角形,AB=3,BC=4.求BD的长;
(3)如图3,若∠ABC=30°,∠ACD=45°,AC=2,B、D之间距离是否有最大值?如有求出最大值;若不存在,说明理由.
-
科目: 来源: 题型:
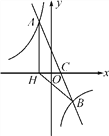
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=
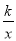 (k≠0)的图象交于A,B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4
(k≠0)的图象交于A,B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4 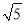 ,cos∠ACH=
,cos∠ACH=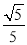 ,点B的坐标为(4,n).
,点B的坐标为(4,n).(1)求该反比例函数和一次函数的解析式;
(2)求△BCH的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 的表达式为
的表达式为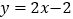 ,直线
,直线 与x轴交于点D,直线
与x轴交于点D,直线 :
: 与x轴交于点A,且经过点B,直线
与x轴交于点A,且经过点B,直线 、
、 交于点
交于点 .
.(1)求m的值;
(2)求直线
 的表达式;
的表达式;(3)根据图象,直接写出
 的解集.
的解集.
相关试题

