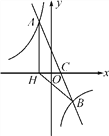
【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() (k≠0)的图象交于A,B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4
(k≠0)的图象交于A,B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4 ![]() ,cos∠ACH=
,cos∠ACH=![]() ,点B的坐标为(4,n).
,点B的坐标为(4,n).
(1)求该反比例函数和一次函数的解析式;
(2)求△BCH的面积.
参考答案:
【答案】(1)y=-![]() ,y=-2x +4;(2)8
,y=-2x +4;(2)8
【解析】试题分析:(1)首先利用锐角三角函数关系得出HC的长,再利用勾股定理得出AH的长,即可得出A点坐标,进而求出反比例函数解析式,再求出B点坐标,即可得出一次函数解析式;
(2)利用B点坐标的纵坐标再利用HC的长即可得出△BCH的面积.
试题解析:
(1)∵AH⊥x轴于点H,
∴∠AHC=90°,
∴CH=AC·cos∠ACH=4![]() ×
×![]() =4,
=4,
∴AH=![]() =8,
=8,
又∵点O是CH的中点,
∴CO=OH=![]() CH=2,
CH=2,
∴点C(2,0),H(-2,0) ,A(-2,8),
把A(-2,8)代入反比例函数的解析式中,得k=-16,
∴反比例函数的解析式为y=-![]() ,
,
把A(-2,8),C(2,0)代入一次函数解析式中,得
![]() 解得
解得![]()
∴一次函数的解析式为y=-2x +4;
(2)将B(4,n)代入y=-![]() 中,得n=-4,
中,得n=-4,
∴S△BCH=![]() ·CH·|yB|=
·CH·|yB|=![]() ×4×4=8.
×4×4=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,先将正方形纸片对折,折痕为EF,再把点C折叠到EF上,折痕为DN,点C在EF上的对应点为M,则下列结论中(1)AM=AB;(2)∠MCE=15°;(3)△AMD是等边三角形;(4)CN=NE,正确的个数有( )
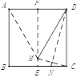
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
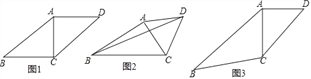
查看答案和解析>>【题目】已知△ABC,以AC为边在△ABC外作等腰△ACD,其中AC=AD.
(1)如图1,若∠DAC=2∠ABC,AC=BC,四边形ABCD是平行四边形,则∠ABC= ;
(2)如图2,若∠ABC=30°,△ACD是等边三角形,AB=3,BC=4.求BD的长;
(3)如图3,若∠ABC=30°,∠ACD=45°,AC=2,B、D之间距离是否有最大值?如有求出最大值;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 的表达式为
的表达式为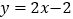 ,直线
,直线 与x轴交于点D,直线
与x轴交于点D,直线 :
: 与x轴交于点A,且经过点B,直线
与x轴交于点A,且经过点B,直线 、
、 交于点
交于点 .
.(1)求m的值;
(2)求直线
 的表达式;
的表达式;(3)根据图象,直接写出
 的解集.
的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从2开始,连续的偶数相加,它们和的情况如下表:

(1)若n=7时,则S的值为___.
(2)根据表中的规律猜想:用n的式子表示S的公式为:S=2+4+6+8+…+2n=___.
根据上题的规律计算:300+302+304+…+2016+2018+2020的值.
-
科目: 来源: 题型:
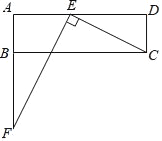
查看答案和解析>>【题目】如图,在矩形ABCD中,已知 AD>AB.在边AD上取点E,连结CE.过点E作EF⊥CE,与边AB的延长线交于点F.
(1)证明:△AEF∽△DCE.
(2)若AB=4,AE=6,AD=14,求线段AF的长.
相关试题

