【题目】如图,直线![]() 的表达式为
的表达式为![]() ,直线
,直线![]() 与x轴交于点D,直线
与x轴交于点D,直线![]() :
:![]() 与x轴交于点A,且经过点B,直线
与x轴交于点A,且经过点B,直线![]() 、
、![]() 交于点
交于点![]() .
.
(1)求m的值;
(2)求直线![]() 的表达式;
的表达式;
(3)根据图象,直接写出![]() 的解集.
的解集.

参考答案:
【答案】(1)点C的坐标为![]() ;(2)直线L2的解析式为y=﹣x+4;(3)
;(2)直线L2的解析式为y=﹣x+4;(3)![]()
【解析】试题分析:(1)把点![]() 的坐标代入直线
的坐标代入直线![]() 的解析式求出
的解析式求出![]() 的值.
的值.
(2)根据点![]() 的坐标,利用待定系数法求一次函数解析式解答;
的坐标,利用待定系数法求一次函数解析式解答;
(3)观察图象,可直接写出![]() 的解集.
的解集.
试题解析:(1)∵点C在直线l1:y=2x2上,
∴2=2m2,m=2,
∴点C的坐标为(2,2);
(2)∵点C(2,2)、B(3,1)在直线l2上,
∴![]()
解之得:![]()
∴直线l2的解析式为y=x+4;
(3)观察图象:
当![]() 时,
时,![]()
![]() 时,
时,![]()
![]() 的解集是:
的解集是:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为8,B是数轴上一点,且AB=14.动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.

(1)写出数轴上点B表示的数 ,点P表示的数 (用含t的代数式表示);
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?
(3)若M为AP的中点,N为PB的中点.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长.
-
科目: 来源: 题型:
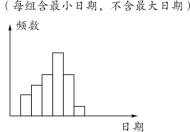
查看答案和解析>>【题目】在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日到30日,评委会把同学们上交作品的件数按5天一组分组统计,绘制了频数分布直方图(如图所示).已知从左至右各长方形的高的比为2∶3∶4∶6∶4∶1,第三组的频数为12,请解答下列问题:
(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?有多少件?
(3)哪组上交的作品数量最少?有多少件?
(4)第二组上交的作品数量是多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】政府计划投资14万亿元实施东进战略.为了解民对东进战略的关注情况,佳佳随机采访部分民,并对采访情况制作了统计图表的一部分如下:
关注情况
频数
频率
A.高度关注
m
0.1
B.一般关注
200
0.5
C.不关注
60
n
D.不知道
100
0.25
(1)采访总人数为__ __人,m=__ __,n=__ __;
(2)补全统计图;
(3)估计在30 000名民中高度关注东进战略的人数约为 人.

-
科目: 来源: 题型:
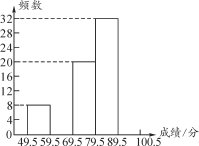
查看答案和解析>>【题目】6月5日是世界环境日,为了普及环保知识,增强环保意识,某市第一中学举行了“环保知识竞赛”,参赛人数为1 000人.为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,最少为50分,得分取整数)进行统计,并绘制出不完整的频数分布表和不完整的频数分布直方图如下:
分组
频数
所占百分比
49.5~59.5
8
8%
59.5~69.5
__ __
12%
69.5~79.5
20
__ __
79.5~89.5
32
__ __
89.5~100.5
__ __
28%
(1)补全频数分布表和频数分布直方图;
(2)若成绩在80分以上为优秀,求这次参赛的学生中成绩为优秀的约有多少人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣4,0),B(2,0),与y轴交于点C(0,2).

(1)求抛物线的解析式;
(2)若点D为该抛物线上的一个动点,且在直线AC上方,当以A,C,D为顶点的三角形面积最大时,求点D的坐标及此时三角形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0( )
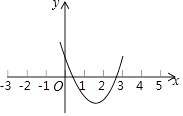
A.没有实根
B.只有一个实根
C.有两个实根,且一根为正,一根为负
D.有两个实根,且一根小于1,一根大于2
相关试题

