【题目】如图,在△ABC中,点O是AC边上的一动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F. 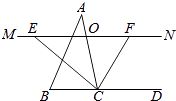
(1)求证:EO=FO;
(2)当CE=12,CF=10时,求CO的长;
(3)当O点运动到何处时,四边形AECF是矩形?并证明你的结论.
参考答案:
【答案】
(1)证明:∵MN∥BC,CE平分∠ACB,CF平分∠ACD,
∴∠BCE=∠ACE=∠OEC,∠OCF=∠FCD=∠OFC,
∴OE=OC,OC=OF,
∴OE=OF
(2)解:∵CE平分∠ACB,CF平分∠ACD,
∴∠ECF= ![]() ∠ACB+
∠ACB+ ![]() ∠ACD=
∠ACD= ![]() ×180°=90°,
×180°=90°,
∴Rt△CEF中,EF= ![]() =
= ![]() =2
=2 ![]() ,
,
又∵OE=OF,
∴CO= ![]() EF=
EF= ![]()
(3)解:当O运动到AC中点时,四边形AECF是矩形,
证明:∵AO=CO,OE=OF,
∴四边形AECF是平行四边形,
由(2)可得∠ECF=90°,
∴四边形AECF是矩形.
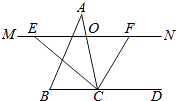
【解析】(1)先根据等角对等边,得出OE=OC,OF=OC,再根据等量代换,得出OE=OF;(2)先根据角平分线的定义,求得∠ECF=90°,再根据勾股定理求得EF的长,最后根据直角三角形的性质,求得CO的长;(3)根据有一个角是直角的平行四边形是矩形矩形判定即可.
【考点精析】本题主要考查了直角三角形斜边上的中线和勾股定理的概念的相关知识点,需要掌握直角三角形斜边上的中线等于斜边的一半;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面的图象反映的过程是:小明从家去超市买文具,又去书店购书,然后回家.其中x表示时间,y表示小明离他家的距离,若小明家、超市、书店在同一条直线上.
根据图象回答下列问题: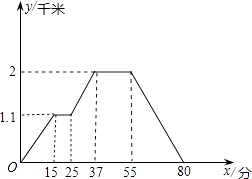
(1)超市离小明家多远,小明走到超市用了多少时间?
(2)超市离书店多远,小明在书店购书用了多少时间?
(3)书店离小明家多远,小明从书店走回家的平均速度是每分钟多少米? -
科目: 来源: 题型:
查看答案和解析>>【题目】(2016湖北襄阳第20题)
如图,直线y=ax+b与反比例函数y=
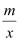 (x>0)的图象交于A(1,4),B(4,n)两点,与x轴,y轴分别交干C,D两点.
(x>0)的图象交于A(1,4),B(4,n)两点,与x轴,y轴分别交干C,D两点.(1)m= ,n= ;若M(xl,y1),N(x2,y2)是反比例函数图象上两点,且0<xl<x2,则yl y2(填“<”或“=”或“>”);
(2)若线段CD上的点P到x轴,y轴的距离相等.求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把方程x(x+1)=2化成一般形式是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=(﹣x)2开口向(填:“上”或“下”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
 的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).(1)求反比例函数与一次函数的表达式;
(2)点E为y轴上一个动点,若S△AEB=5,求点E的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市“全国文明村”白村果农王保收获枇杷20吨,桃子12吨.现计划租用甲、乙两种货车共8辆将这批水果全部运往外地销售,已知一辆甲种货车可装枇杷4吨和桃子1吨,一辆乙种货车可装枇杷和桃子各2吨.
(1)王保如何安排甲、乙两种货车可一次性地运到销售地?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果农王保应选择哪种方案,使运输费最少?最少运费是多少?
相关试题

