【题目】某市“全国文明村”白村果农王保收获枇杷20吨,桃子12吨.现计划租用甲、乙两种货车共8辆将这批水果全部运往外地销售,已知一辆甲种货车可装枇杷4吨和桃子1吨,一辆乙种货车可装枇杷和桃子各2吨.
(1)王保如何安排甲、乙两种货车可一次性地运到销售地?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果农王保应选择哪种方案,使运输费最少?最少运费是多少?
参考答案:
【答案】(1)设安排甲种货车x辆,则安排乙种货车(8-x)辆,依题意,得:![]()
解之得:![]()
即![]()
∵车辆数x只能为正整数
∴x=2,3,4
因此安排甲、乙两种货车有三种方案:
甲种货车 | 乙种货车 | |
方案一 | 2辆 | 6辆 |
方案二 | 3辆 | 5辆 |
方案三 | 4辆 | 4辆 |
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则上述三种方案各需运费金额为:
方案一:甲种货车2辆、乙种货车6辆:运费为300×2+240×6=2040元;
方案二:甲种货车3辆、乙种货车5辆:运费为300×3+240×5=2100元;
方案三:甲种货车4辆、乙种货车4辆:运费为300×4+240×4=2160元;
三种方案所需运费比较可知,方案一的运费最少,最少运费是2040元。
【解析】抽取关系列不等式组,应用题的结果往往要符合现实意义,不等式组可以把所有可能的结果呈现出来。
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(3a+6,3-a)关于x轴的对称点在第四象限内,则a的取值范围为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的不等式mx-1>0(m≠0)的解集是x>1,则直线y=mx-1与x轴的交点坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
 ,并在数轴上表示出其解集.
,并在数轴上表示出其解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】用“>”或“<”填空:若a<b,则﹣2a+1__﹣2b+1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE∥BD,过点D作ED∥AC,两线相交于点E.
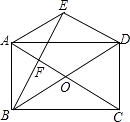
(1)求证:四边形AODE是菱形;
(2)连接BE,交AC于点F.若BE⊥ED于点E,求∠AOD的度数. -
科目: 来源: 题型:
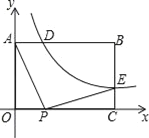
查看答案和解析>>【题目】如图,已知矩形OABC中,OA=3,AB=4,双曲线y=
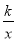 (k>0)与矩形两边AB、BC分别交于D、E,且BD=2AD
(k>0)与矩形两边AB、BC分别交于D、E,且BD=2AD(1)求k的值和点E的坐标;
(2)点P是线段OC上的一个动点,是否存在点P,使∠APE=90°?若存在,求出此时点P的坐标,若不存在,请说明理由.
相关试题

