【题目】(1)甲、乙、丙、丁四人做传球游戏:第一次由甲将球随机传给乙、丙、丁中的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人中的某一人.
(1)求第二次传球后球回到甲手里的概率.(请用“画树状图”或“列表”等方式给出分析过程)
(2)如果甲跟另外n(n≥2)个人做(1)中同样的游戏,那么,第三次传球后球回到甲手里的概率是
参考答案:
【答案】
(1)
解:画树状图:
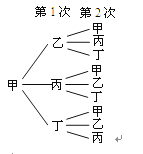
共有9种等可能的结果,其中符合要求的结果有3种,
∴P(第2次传球后球回到甲手里)=![]() =
=![]() .
.
(2)![]()
【解析】(2)第三步传的结果是n3 , 传给甲的结果是n(n﹣1),
第三次传球后球回到甲手里的概率是![]() =
=![]() ,
,
所以答案是:![]() .
.
【考点精析】本题主要考查了列表法与树状图法的相关知识点,需要掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB∥CD,E是AB的中点,CE=DE.

(1)求证:∠AEC=∠BED
(2)求证:AC=BD -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.

(1)求BD的长
(2)求图中阴影部分的面积 -
科目: 来源: 题型:
查看答案和解析>>【题目】某区教研部门对本区初二年级的学生进行了一次随机抽样问卷调查,其中有这样一个问题:
老师在课堂上放手让学生提问和表达,
A.从不 B.很少 C.有时 D.常常 E.总是
答题的学生在这五个选项中只能选择一项.如图是根据学生对该问题的答卷情况绘制的两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)该区共有 名初二年级的学生参加了本次问卷调查
(2)请把这幅条形统计图补充完整
(3)在扇形统计图中,“总是”所占的百分比为 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:平面直角坐标系中,四边形OABC的顶点分别为O(0,0)、A(5,0)、B(m,2)、C(m﹣5,2).
(1)问:是否存在这样的m,使得在边BC上总存在点P,使∠OPA=90°?若存在,求出m的取值范围;若不存在,请说明理由.
(2)当∠AOC与∠OAB的平分线的交点Q在边BC上时,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=
 x的图象如图所示,它与二次函数y=ax2﹣4ax+c的图象交于A、B两点(其中点A在点B的左侧),与这个二次函数图象的对称轴交于点C.
x的图象如图所示,它与二次函数y=ax2﹣4ax+c的图象交于A、B两点(其中点A在点B的左侧),与这个二次函数图象的对称轴交于点C.
(1)求点C的坐标
(2)设二次函数图象的顶点为D.
①若点D与点C关于x轴对称,且△ACD的面积等于3,求此二次函数的关系式;
②若CD=AC,且△ACD的面积等于10,求此二次函数的关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.

(1)若∠AOB=60°,OM=4,OQ=1,求证:CN⊥OB
(2)当点N在边OB上运动时,四边形OMPQ始终保持为菱形.
①问: ﹣
﹣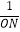 的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.
的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.
②设菱形OMPQ的面积为S1 , △NOC的面积为S2 , 求 的取值范围.
的取值范围.
相关试题

