【题目】已知:直线y=﹣x﹣4分别交x、y轴于A、C两点,抛物线y=ax2+bx(a>0)经过A、O两点,且顶点B的纵坐标为﹣2 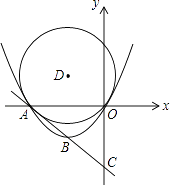
(1)判断点B是否在直线AC上,并求该抛物线的函数关系式;
(2)以点B关于x轴的对称点D为圆心,以OD为半径作⊙D,试判断直线AC与⊙D的位置关系,并说明理由;
(3)若E为⊙D的优弧AO上一动点(不与A、O重合),连结AE、OE,问在抛物线上是否存在点P,使∠POA:∠AEO=2:3?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)解:∵点A、C分别是直线y=﹣x﹣4与x、y轴的交点,
∴点A(﹣4,0),点C(0,﹣4),
由题意可得:  ,
,
解得 ![]() ,
,
∴抛物线的函数关系式为y= ![]() x2+2x.
x2+2x.
由y= ![]() x2+2x=
x2+2x= ![]() (x+2)2﹣2得顶点B(﹣2,﹣2).
(x+2)2﹣2得顶点B(﹣2,﹣2).
当x=﹣2时,y=﹣x﹣4=﹣2,
∴点B在直线y=﹣x﹣4上
(2)解:直线AC与⊙D相切.
理由:连接DA,如图1.
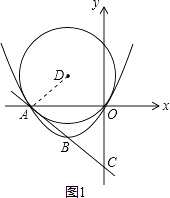
∵A(﹣4,0),C(0,﹣4),
∴OA=OC=4.
∵∠AOC=90°,
∴∠OAC=∠OCA=45°.
∵点B在直线AC上,
∴∠BAO=45°.
∵点B与点D关于x轴对称,
∴∠DAO=∠BAO=45°,
∴∠DAB=90°,
∵抛物线y=ax2+bx(a>0)经过A、O两点,顶点是B,点B与点D关于x轴对称,OD为半径,
∴直线AC与⊙D相切
(3)解:过点P作PH⊥x轴于H,如图2①、图2②,


∵DA=DO,
∴∠DOA=∠DAO=45°,
∴∠ADO=90°.
∵E为⊙D的优弧AO上一动点(不与A、O重合),
∴∠AEO= ![]() ∠ADO=45°.
∠ADO=45°.
∵∠POA:∠AEO=2:3,
∴∠POA= ![]() ∠AEO=
∠AEO= ![]() ×45°=30°.
×45°=30°.
∴直线OP的解析式为y= ![]() x,或y=﹣
x,或y=﹣ ![]() x.
x.
①当直线OP的解析式为y=﹣ ![]() x时,如图2①,
x时,如图2①,
解方程组  ,得
,得
![]() 或
或 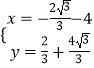 ,
,
∴点P的坐标为(﹣ ![]() ﹣4,
﹣4, ![]() +
+ ![]() ).
).
②当直线OP的解析式为y= ![]() x时,如图2②,
x时,如图2②,
解方程组  ,得
,得
![]() 或
或 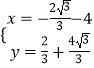 ,
,
∴点P的坐标为( ![]() ,
, ![]() ).
).
综上所述:点P的坐标为(﹣ ![]() ﹣4
﹣4 ![]() )或(
)或( ![]() -4,
-4, ![]() ).
).
【解析】(1)可先求出点A、C的坐标,然后结合点A的坐标及顶点B的纵坐标为﹣2可得到关于a、b的方程组,然后解这个方程组,就可得到抛物线的函数关系式,从而得到点B的坐标,然后把点B的坐标代入直线AC的解析式,就可解决问题;(2)连接DA,如图1,要证直线AC与⊙D相切,只需证∠DAC=90°;(3)过点P作PH⊥x轴于H,如图2①、图2②,易得∠ADO=90°,根据圆周角定理可得∠AEO,从而求出∠POA,从而可得到直线OP的解析式,然后解直线OP与抛物线的解析式组成的方程组,就可得到点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为提倡全民健身活动, 某社区准备购买羽毛球和羽毛球拍供社区居民使用, 某体育用品商店羽毛球每盒 10 元, 羽毛球拍每副 40 元 .该商店有两种优惠方案,方案一: 不购买会员卡时, 羽毛球享受 8.5 折优惠, 羽毛球拍购买 5 副(含5 副) 以上才能享受 8.5 折优惠, 5 副以下必须按定价购买;方案二: 每张会员卡 20 元, 办理会员卡时, 全部商品享受 8 折优惠 . 设该社区准备购买羽毛球拍 6 副, 羽毛球
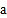 盒, 请回答下列问题:
盒, 请回答下列问题:(1)如果一位体育爱好者按方案一只购买了 4 副羽毛球拍,求他购买时所需要的费用;
(2)用含
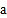 的代数式分别表示该社区按方案一和方案二购买所需要的钱数;
的代数式分别表示该社区按方案一和方案二购买所需要的钱数;(3)①直接写出一个
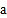 的值, 使方案一比方案二优惠;
的值, 使方案一比方案二优惠;②直接写出一个
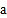 的值, 使方案二比方案一优惠 .
的值, 使方案二比方案一优惠 . -
科目: 来源: 题型:
查看答案和解析>>【题目】2016年2月18日韩国海军海警在朝鲜半岛东部海域实施联合演习,在返回济州岛军事基地途中,韩国海军UH﹣60直升机在距海平面垂直高度为300米的点C处测得济州一小岛的西端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了3500米,在点D测得这小岛的东端点B的俯角为45°,求这个济州小岛东西两端BA的距离(结果精确到1米,参考数据:
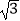 ≈1.732,
≈1.732, 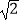 ≈1.414)
≈1.414)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=x+3分别交x,y轴于点D,C,点B在x轴上,OB=OC,过点B作直线m∥CD.点P、Q分别为直线m和直线CD上的动点,且点P在x轴的上方,满足∠POQ=45°
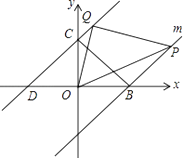
(1)则∠PBO=度;
(2)问:PBCQ的值是否为定值?如果是,请求出该定值;如果不是,请说明理由;
(3)求证:CQ2+PB2=PQ2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,过点C作CD⊥CB交∠CBA的外角平分线于点D,连接AD,过点C作∠BCE=∠BAD,交AB的延长线于点E.若CD=3,则CE=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】五一期间刚到深圳的小明在哥哥的陪伴下,打算上午从莲山春早、侨城锦绣、深南溢彩中随机选择一个景点,下午从梧桐烟云、梅沙踏浪、一街两制中随机选择一个景点,小明恰好上午选中莲山春早,下午选中梅沙踏浪的概率是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中AB=3,BC=4,∠B=90°,点B、C在两坐标轴上滑动.当边AC⊥x轴时,点A刚好在双曲线
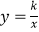 上,此时下列结论不正确的是( )
上,此时下列结论不正确的是( )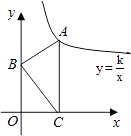
A.点B为(0,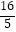 )
)
B.AC边的高为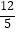
C.双曲线为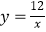
D.此时点A与点O距离最大
相关试题

