搜索
【题目】已知：线段AB=40cm.
(1)如图①，点P沿线段AB自点A向点B以3厘米/秒运动，同时点Q线段BA自B点向点A以5厘米/秒运动，问经过几秒后P、Q相遇？
(2)几秒钟后，P、Q相距16厘米？
(3)如图②，AO=PO=8厘米，∠POB=40°，点P绕点O以20度/秒的速度顺时针旋转一周停止，同时点Q沿直线BA自B点向点A运动，假若P、Q两点能相遇，求Q运动的速度.
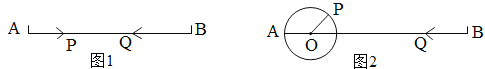
参考答案：
【答案】(1)经过5秒钟后P、Q相遇；(2)经过3秒钟或7秒钟后，P、Q相距16cm；(3)点Q运动的速度为12cm/s或
cm/s.
【解析】
（1）根据相遇时，点P和点Q的运动的路程和等于AB的长列方程即可求解；
（2）设经过xs，P、Q两点相距10cm，分相遇前和相遇后两种情况建立方程求出其解即可；
（3）由于点P，Q只能在直线AB上相遇，而点P旋转到直线AB上的时间分两种情况，所以根据题意列出方程分别求解．
(1)设经过ts后，点P、Q相遇,
依题意，有3t+5t=40，
解得t=5.
答：经过5秒钟后P、Q相遇；
(2)设经过xs，P、Q两点相距16cm，由题意得
3x+5x+16=40或3x+5x16=40，
解得：x=3或x=7.
答：经过3秒钟或7秒钟后，P、Q相距16cm；
(3)点P，Q只能在直线AB上相遇，
则点P旋转到直线AB上的时间为40÷20=2s或(40+180)÷20=11s.
设点Q的速度为ycm/s,则有2y=4016,解得y=12或11y=40,解得
答：点Q运动的速度为12cm/s或cm/s.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图：抛物线
与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C．点P为线段BC上一点，过点P作直线ι⊥x轴于点F，交抛物线 
于点E．
（1）求A、B、C三点的坐标；
（2）当点P在线段BC上运动时，求线段PE长的最大值；
（3）当PE取最大值时，把抛物线 向右平移得到抛物线 
，抛物线 与线段BE交于点M，若直线CM把△BCE的面积分为1：2两部分，则抛物线 应向右平移几个单位长度可得到抛物线 ？ -
科目： 来源： 题型：
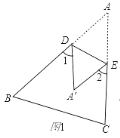
查看答案和解析>>【题目】(1)如图1，把△ABC沿DE折叠，使点A落在点A’处，试探索∠1+∠2与∠A的关系．（证明）．
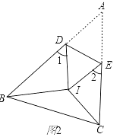
(2)如图2，BI平分∠ABC，CI平分∠ACB，把△ABC折叠，使点A与点I重合，若∠1+∠2=130°，求∠BIC的度数；
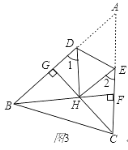
(3)如图3，在锐角△ABC中，BF⊥AC于点F，CG⊥AB于点G，BF、CG交于点H，把△ABC折叠使点A和点H重合，试探索∠BHC与∠1+∠2的关系，并证明你的结论．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图：为了测量某棵树的高度，小刚用长为2m的竹竿做测量工具，移动竹竿，使竹竿、树的顶端的影子恰好落在地面的同一点，此时，竹竿与这一点距离6m，与树相距15m，那么这棵的高度为（ ）
A.5米
B.7米
C.7．5米
D.21米 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知∠AOB＝130°，∠COD＝80°，OM，ON分别是∠AOB和∠COD的平分线．
(1)如果OA，OC重合，且OD在∠AOB的内部，如图1，求∠MON的度数；
(2)如果将图1中的∠COD绕点O点顺时针旋转n°(0＜n＜155)，如图2，
①∠MON与旋转度数n°有怎样的数量关系？说明理由；
②当n为多少时，∠MON为直角？
(3)如果∠AOB的位置和大小不变，∠COD的边OD的位置不变，改变∠COD的大小；将图1中的OC绕着O点顺时针旋转m°(0＜m＜100)，如图3，∠MON与旋转度数m°有怎样的数量关系？说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的切线，B为切点，AO的延长线交⊙O于点C，连接BC，如果∠A=30°，AB=2
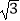，那么AC的长等于（ ）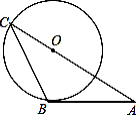
A.4
B.6
C.4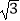
D.6 -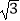
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，AD，BC是⊙O的两条互相垂直的直径，点P从点O出发沿图中某一个扇形顺时针匀速运动，设∠APB=y（单位：度），如果y与点P运动的时间x（单位：秒）的函数关系的图象大致如图2所示，那么点P的运动路线可能为（ ）
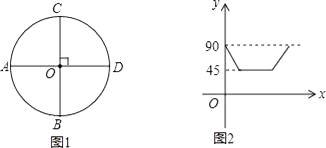
A.O→B→A→O
B.O→A→C→O
C.O→C→D→O
D.O→B→D→O
相关试题
