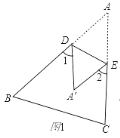
【题目】(1)如图1,把△ABC沿DE折叠,使点A落在点A’处,试探索∠1+∠2与∠A的关系.(证明).
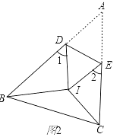
(2)如图2,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=130°,求∠BIC的度数;
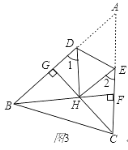
(3)如图3,在锐角△ABC中,BF⊥AC于点F,CG⊥AB于点G,BF、CG交于点H,把△ABC折叠使点A和点H重合,试探索∠BHC与∠1+∠2的关系,并证明你的结论.
参考答案:
【答案】(1)∠1+∠2=2∠A;(2)122.5°;(3)∠BHC=180°-![]() (∠1+∠2).
(∠1+∠2).
【解析】
(1)根据翻折变换的性质以及三角形内角和定理以及平角的定义求出即可;
(2)根据三角形角平分线的性质得出∠IBC+∠ICB=90°-![]() ∠A,得出∠BIC的度数即可;
∠A,得出∠BIC的度数即可;
(3)根据翻折变换的性质以及垂线的性质得出,∠AFH+∠AGH=90°+90°=180°,进而求出∠A=![]() (∠1+∠2),即可得出答案.
(∠1+∠2),即可得出答案.
(1)∠1+∠2=2∠A;
∵∠A+∠A′+∠A′DA+∠A′EA=360°
又∵∠1+∠A′DA+∠2+∠AEA′=360°
∴∠A+∠A′=∠1+∠2
又∵∠A=∠A′
∴2∠A=∠1+∠2.
(2)由(1)∠1+∠2=2∠A,得2∠A=130°,∴∠A=65°
∵IB平分∠ABC,IC平分∠ACB,
∴∠IBC+∠ICB=![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
=![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() ∠A,
∠A,
∴∠BIC=180°-(∠IBC+∠ICB),
=180°-(90°-![]() ∠A)=90°+
∠A)=90°+![]() ×65°=122.5°;
×65°=122.5°;
(3)∵BF⊥AC,CG⊥AB,∴∠AFH+∠AGH=90°+90°=180°,
∠FHG+∠A=180°,∴∠BHC=∠FHG=180°-∠A,由(1)知∠1+∠2=2∠A,
∴∠A=![]() (∠1+∠2),
(∠1+∠2),
∴∠BHC=180°-![]() (∠1+∠2).
(∠1+∠2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,长方形纸片ABCD的长AD=9cm,宽AB=3cm,将其折叠,使点D与点B重合.
求:(1)折叠后DE的长;(2)以折痕EF为边的正方形面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,E是圆内的两条弦AB、CD的交点,直线EF∥CB,交AD的延长线于F,FG切圆于G.连接AG、DG.

求证:
(1)△DFE∽△EFA
(2)EF=FG -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:抛物线
 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.点P为线段BC上一点,过点P作直线ι⊥x轴于点F,交抛物线
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.点P为线段BC上一点,过点P作直线ι⊥x轴于点F,交抛物线  于点E.
于点E.
(1)求A、B、C三点的坐标;
(2)当点P在线段BC上运动时,求线段PE长的最大值;
(3)当PE取最大值时,把抛物线 向右平移得到抛物线
向右平移得到抛物线  ,抛物线
,抛物线  与线段BE交于点M,若直线CM把△BCE的面积分为1:2两部分,则抛物线
与线段BE交于点M,若直线CM把△BCE的面积分为1:2两部分,则抛物线  应向右平移几个单位长度可得到抛物线
应向右平移几个单位长度可得到抛物线  ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:为了测量某棵树的高度,小刚用长为2m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点,此时,竹竿与这一点距离6m,与树相距15m,那么这棵的高度为( )

A.5米
B.7米
C.7.5米
D.21米 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:线段AB=40cm.
(1)如图①,点P沿线段AB自点A向点B以3厘米/秒运动,同时点Q线段BA自B点向点A以5厘米/秒运动,问经过几秒后P、Q相遇?
(2)几秒钟后,P、Q相距16厘米?
(3)如图②,AO=PO=8厘米,∠POB=40°,点P绕点O以20度/秒的速度顺时针旋转一周停止,同时点Q沿直线BA自B点向点A运动,假若P、Q两点能相遇,求Q运动的速度.
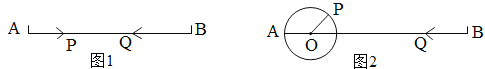
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=130°,∠COD=80°,OM,ON分别是∠AOB和∠COD的平分线.
(1)如果OA,OC重合,且OD在∠AOB的内部,如图1,求∠MON的度数;
(2)如果将图1中的∠COD绕点O点顺时针旋转n°(0<n<155),如图2,
①∠MON与旋转度数n°有怎样的数量关系?说明理由;
②当n为多少时,∠MON为直角?
(3)如果∠AOB的位置和大小不变,∠COD的边OD的位置不变,改变∠COD的大小;将图1中的OC绕着O点顺时针旋转m°(0<m<100),如图3,∠MON与旋转度数m°有怎样的数量关系?说明理由.

相关试题

