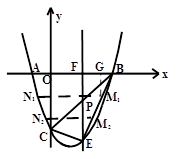
【题目】如图:抛物线 ![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.点P为线段BC上一点,过点P作直线ι⊥x轴于点F,交抛物线
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.点P为线段BC上一点,过点P作直线ι⊥x轴于点F,交抛物线 ![]() 于点E.
于点E.
(1)求A、B、C三点的坐标;
(2)当点P在线段BC上运动时,求线段PE长的最大值;
(3)当PE取最大值时,把抛物线 ![]() 向右平移得到抛物线
向右平移得到抛物线 ![]() ,抛物线
,抛物线 ![]() 与线段BE交于点M,若直线CM把△BCE的面积分为1:2两部分,则抛物线
与线段BE交于点M,若直线CM把△BCE的面积分为1:2两部分,则抛物线 ![]() 应向右平移几个单位长度可得到抛物线
应向右平移几个单位长度可得到抛物线 ![]() ?
?
参考答案:
【答案】
(1)解:当x=0时,y=-3,C(0,-3),
当y=0时, ![]()
解得 ![]() ,
, ![]() ,
,
A(-1,0),B(3,0)
(2)解:直线BC的解析式为 ![]() ,则P(x,x-3)(0≦x≦3) E
,则P(x,x-3)(0≦x≦3) E ![]() .
.
PE= ![]() =
= ![]()
![]() 当
当 ![]() 时,PE最大值=
时,PE最大值= ![]()
(3)解:E ![]() ,直线BE的解析式为
,直线BE的解析式为 ![]()
![]() 直线CM把△BCE的面积分成1:2.
直线CM把△BCE的面积分成1:2.
![]() M为BE的三等分点,有两种情况如图:
M为BE的三等分点,有两种情况如图:
① ![]() 和
和 ![]() ,过
,过 ![]() 作
作 ![]() 于G,
于G,
则 ![]()
![]()
![]()
![]()
![]()
![]() 同理
同理 ![]()
方法一:设抛物线 ![]() 为
为 ![]()
①当抛物线 ![]() 过点
过点 ![]() 时,
时, ![]() 解得:
解得:
![]() 或
或 ![]() <0(舍去)
<0(舍去)
②当抛物线 ![]() 过点
过点 ![]() 时,
时, ![]() 解得:
解得: ![]() 或
或 ![]() <0(舍去)
<0(舍去)
综上所述:把抛物线 ![]() 向右平移
向右平移 ![]() 或
或 ![]() 个单位长度,就能得到抛物线
个单位长度,就能得到抛物线 ![]() .
.
方法二:过点 ![]() 作
作 ![]() //x轴交抛物线
//x轴交抛物线 ![]() 对称轴左侧于
对称轴左侧于 ![]()
当 ![]() 时,
时, ![]() 解得:
解得: ![]() 或
或 ![]() >1(舍去)
>1(舍去)
![]()
过点 ![]() 作
作 ![]() //x轴交抛物线
//x轴交抛物线 ![]() 对称轴左侧于
对称轴左侧于 ![]()
当 ![]() 时,
时, ![]()
解得: ![]() 或
或 ![]() >1(舍去)
>1(舍去)
![]()
综上所述:把抛物线 ![]() 向右平移
向右平移 ![]() 或
或 ![]() 个单位长度,就能得到抛物线
个单位长度,就能得到抛物线 ![]() .
.
【解析】(1)将x=0代入函数解析式求出对应的函数值,就可求出点C的坐标,再由y=0,求出对应的自变量的值,就可得出点A、B的坐标。
(2)利用待定系数法求出直线BC的函数解析式,根据直线ι⊥x轴可知直线l与y轴平行,则F、P、E三点的横坐标相等,设出点P的坐标,就可表示出点E的坐标。因此PE的长=点P的纵坐标与点E的纵坐标之差,列出PE与x的函数关系式,再求出其顶点坐标,根据函数的性质即可得出PE的最大值。
(3)先用平移的单位设出c2的解析式.由于直线CM把△BCE的面积分为1:2两部分,根据等高三角形的面积比等于底边比,可得出ME:BE=1:2或2:1.因此本题要分两种情况进行讨论,可过M作x轴的垂线,先根据相似三角形求出M点的横坐标,然后根据直线BE的解析式,求出M点的坐标.由于抛物线c2经过M点,据此可求出抛物线需要平移的单位。
【考点精析】解答此题的关键在于理解二次函数的最值的相关知识,掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四川雅安发生地震后,某校学生会向全校1900名学生发起了“心系雅安”捐款活动,为了解捐款情况,学会生随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列是问题:

(1)本次接受随机抽样调查的学生人数为 ,图①中m的值是 ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,长方形纸片ABCD的长AD=9cm,宽AB=3cm,将其折叠,使点D与点B重合.
求:(1)折叠后DE的长;(2)以折痕EF为边的正方形面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,E是圆内的两条弦AB、CD的交点,直线EF∥CB,交AD的延长线于F,FG切圆于G.连接AG、DG.

求证:
(1)△DFE∽△EFA
(2)EF=FG -
科目: 来源: 题型:
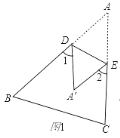
查看答案和解析>>【题目】(1)如图1,把△ABC沿DE折叠,使点A落在点A’处,试探索∠1+∠2与∠A的关系.(证明).
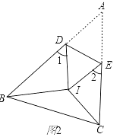
(2)如图2,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=130°,求∠BIC的度数;
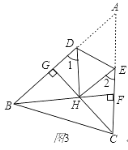
(3)如图3,在锐角△ABC中,BF⊥AC于点F,CG⊥AB于点G,BF、CG交于点H,把△ABC折叠使点A和点H重合,试探索∠BHC与∠1+∠2的关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:为了测量某棵树的高度,小刚用长为2m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点,此时,竹竿与这一点距离6m,与树相距15m,那么这棵的高度为( )

A.5米
B.7米
C.7.5米
D.21米 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:线段AB=40cm.
(1)如图①,点P沿线段AB自点A向点B以3厘米/秒运动,同时点Q线段BA自B点向点A以5厘米/秒运动,问经过几秒后P、Q相遇?
(2)几秒钟后,P、Q相距16厘米?
(3)如图②,AO=PO=8厘米,∠POB=40°,点P绕点O以20度/秒的速度顺时针旋转一周停止,同时点Q沿直线BA自B点向点A运动,假若P、Q两点能相遇,求Q运动的速度.
相关试题

