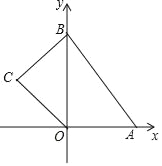
【题目】如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A的坐标为(6,0),点B的坐标为(0,8),点C的坐标为(﹣2![]() ,4),点M,N分别为四边形OABC边上的动点,动点M从点O开始,以每秒1个单位长度的速度沿O→A→B路线向终点B匀速运动,动点N从O点开始,以每秒两个单位长度的速度沿O→C→B→A路线向终点A匀速运动,点M,N同时从O点出发,当其中一点到达终点后,另一点也随之停止运动,设动点运动的时间t秒(t>0),△OMN的面积为S.
,4),点M,N分别为四边形OABC边上的动点,动点M从点O开始,以每秒1个单位长度的速度沿O→A→B路线向终点B匀速运动,动点N从O点开始,以每秒两个单位长度的速度沿O→C→B→A路线向终点A匀速运动,点M,N同时从O点出发,当其中一点到达终点后,另一点也随之停止运动,设动点运动的时间t秒(t>0),△OMN的面积为S.
(1)填空:AB的长是 ,BC的长是 ;
(2)当t=3时,求S的值;
(3)当3<t<6时,设点N的纵坐标为y,求y与t的函数关系式;
(4)若S=![]() ,请直接写出此时t的值.
,请直接写出此时t的值.
参考答案:
【答案】(1)10,6(2)6(3)y=![]() t(4)若S=
t(4)若S=![]() ,此时t的值8s或
,此时t的值8s或![]() s或
s或![]() s
s
【解析】
试题分析:(1)利用勾股定理即可解决问题;
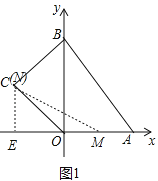
(2)如图1中,作CE⊥x轴于E.连接CM.当t=3时,点N与C重合,OM=3,易求△OMN的面积;
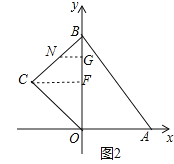
(3)如图2中,当3<t<6时,点N在线段BC上,BN=12﹣2t,作NG⊥OB于G,CF⊥OB于F.则F(0,4).由GN∥CF,推出![]() ,即
,即![]() ,可得BG=8﹣
,可得BG=8﹣![]() t,由此即可解决问题;
t,由此即可解决问题;
(4)分三种情形①当点N在边长上,点M在OA上时.②如图3中,当M、N在线段AB上,相遇之前.作OE⊥AB于E,则OE=![]() =
=![]() ,列出方程即可解决问题.③同法当M、N在线段AB上,相遇之后,列出方程即可;
,列出方程即可解决问题.③同法当M、N在线段AB上,相遇之后,列出方程即可;
试题解析:(1)在Rt△AOB中,∵∠AOB=90°,OA=6,OB=8,∴AB=![]() =
=![]() =10.
=10.
BC=![]() =6.
=6.
(2)如图1中,作CE⊥x轴于E.连接CM.
∵C(﹣![]() ,4),∴CE=4OE=
,4),∴CE=4OE=![]() ,在Rt△COE中,OC=
,在Rt△COE中,OC=![]() =
=![]() =6,当t=3时,点N与C重合,OM=3,∴S△ONM=
=6,当t=3时,点N与C重合,OM=3,∴S△ONM=![]() OMCE=
OMCE=![]() ×3×4=6,即S=6.
×3×4=6,即S=6.
(3)如图2中,当3<t<6时,点N在线段BC上,BN=12﹣2t,作NG⊥OB于G,CF⊥OB于F.则F(0,4).∵OF=4,OB=8,∴BF=8﹣4=4,∵GN∥CF,∴![]() ,即
,即![]() ,∴BG=8﹣
,∴BG=8﹣![]() t,∴y=OB﹣BG=8﹣(8﹣
t,∴y=OB﹣BG=8﹣(8﹣![]() t)=
t)=![]() t.
t.
(4)①当点N在边长上,点M在OA上时,![]()
![]() tt=
tt=![]() ,解得t=
,解得t=![]() (负根已经舍弃).
(负根已经舍弃).
②如图3中,当M、N在线段AB上,相遇之前.
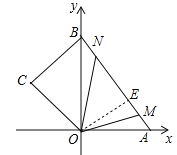
作OE⊥AB于E,则OE=![]() =
=![]() ,由题意
,由题意![]() [10﹣(2t﹣12)﹣(t﹣6)]
[10﹣(2t﹣12)﹣(t﹣6)] ![]() =
= ![]() ,解得t=8,同法当M、N在线段AB上,相遇之后.
,解得t=8,同法当M、N在线段AB上,相遇之后.
由题意![]() [(2t﹣12)+(t﹣6)﹣10]
[(2t﹣12)+(t﹣6)﹣10] ![]() =
= ![]() ,解得t=
,解得t=![]() .
.
综上所述,若S=![]() ,此时t的值8s或
,此时t的值8s或![]() s或
s或![]() s.
s.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1过点A(0,4),点D(4,0),直线l2:
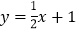 与x轴交于点C,两直线
与x轴交于点C,两直线 ,
, 相交于点B.
相交于点B.(1)求直线
 的解析式和点B的坐标;
的解析式和点B的坐标;(2)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某文物古迹遗址每周都吸引大量中外游客前来参观,如果游客过多,对文物古迹会产生不良影响,但同时考虑到文物的修缮和保存费用的问题,还要保证有一定的门票收入,因此遗址的管理部门采取了升、降门票价格的方法来控制参观人数.在实施过程中发现:每周参观人数y(人)与票价x(元)之间怡好构成一次函数关系.
(Ⅰ)根据题意完成下列表格
票价x(元)
10
15
x
18
参观人数y(人)
7000
4500
(Ⅱ)在这样的情况下,如果要确保每周有40000元的门票收入,那么每周应限定参观人数是多少?门票价格应定位多少元?
(Ⅲ)门票价格应该是多少元时,门票收入最大?这样每周应有多少人参观?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大酒店客房部有三人间、双人间和单人间客房,收费数据如下表(例如三人间普通间客房每人每天收费50元).为吸引客源,在“十一黄金周”期间进行优惠大酬宾,凡团体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间、双人间普通客房,并且每个客房正好住满,一天一共花去住宿费1510元.
普通间(元/人/天)
豪华间(元/人/天)
贵宾间(元/人/天)
三人间
50
100
500
双人间
70
150
800
单人间
100
200
1500
(1)三人间、双人间普通客房各住了多少间?
(2)设三人间共住了x人,则双人间住了 人,一天一共花去住宿费用y元表示,写出y与x的函数关系式;
(3)如果你作为旅游团团长,你认为上面这种住宿方式是不是费用最少?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某高校共有5个大餐厅和2个小餐厅。经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐。
(1)1个大餐厅和1个小餐厅分别可供多少名学生就餐?
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,EF⊥AC于F,DB⊥AC于M,∠1=∠2,∠3=∠C.
(1)求证:AB//MN.
(2)若∠C=40°,∠MND=100°,求∠CAD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线l1与l2形状相同,开口方向不同,其中抛物线l1:y=ax2﹣8ax﹣
 交x轴于A,B两点(点A在点B的左侧),且AB=6;抛物线l2与l1交于点A和点C(5,n).
交x轴于A,B两点(点A在点B的左侧),且AB=6;抛物线l2与l1交于点A和点C(5,n).(1)求抛物线l1,l2的表达式;
(2)当x的取值范围是 时,抛物线l1与l2上的点的纵坐标同时随横坐标的增大而增大;
(3)直线MN∥y轴,交x轴,l1,l2分别相交于点P(m,0),M,N,当1≤m≤7时,求线段MN的最大值.
相关试题

