【题目】如图,直线l1过点A(0,4),点D(4,0),直线l2:![]() 与x轴交于点C,两直线
与x轴交于点C,两直线![]() ,
,![]() 相交于点B.
相交于点B.
(1)求直线![]() 的解析式和点B的坐标;
的解析式和点B的坐标;
(2)求△ABC的面积.

参考答案:
【答案】(1)直线![]() 的解析式为y=-x+4,点B的坐标为(2,2);(2)
的解析式为y=-x+4,点B的坐标为(2,2);(2)![]() .
.
【解析】(1)根据题意l1经过A、B两点,又直线的解析式为y=ax+b,代入可得a、b的值.
(2)由图可知△ACB的面积为△ACD与△CBD的差,所以求得△ACD与△BCD的面积即可知△ACB的面积.
(1)设l1的解析式为:y=ax+b.
∵l1经过A(0,4),D(4,0),
∴将A、D代入解析式得:b=4,4a+b=0,
∴a=﹣1,b=4.
即l1的解析式为:y=﹣x+4,
l1与l2联立 ,得:B(2,2);
,得:B(2,2);
(2)C是l2与x轴的交点,在y=![]() x+1中所以令y=0,得:C(﹣2,0),
x+1中所以令y=0,得:C(﹣2,0),
∴|CD|=6,|AO|=4,B到x轴的距离为2.
∵AO⊥CD,
∴△ACD的面积为![]() |AO||CD|=
|AO||CD|=![]() ×4×6=12 ,
×4×6=12 ,
△CBD的面积为![]() ×B到x轴的距离×CD=
×B到x轴的距离×CD=![]() ×2×6=6 ,
×2×6=6 ,
∴△ABC的面积=△ACD的面积-△CBD的面积=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在《九章算术》中有求三角形面积公式“底乘高的一半”,但是在实际丈量土地面积时,量出高并非易事,所以古人想到了能否利用三角形的三条边长来求面积.我国南宋著名的数学家秦九韶(
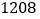 年—
年— 年)提出了“三斜求积术”,阐述了利用三角形三边长求三角形面积方法,简称秦九韶公式.在海伦(公元
年)提出了“三斜求积术”,阐述了利用三角形三边长求三角形面积方法,简称秦九韶公式.在海伦(公元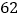 年左右,生平不详)的著作《测地术》中也记录了利用三角形三边长求三角形面积的方法,相传这个公式最早是由古希腊数学家阿基米德(公元前
年左右,生平不详)的著作《测地术》中也记录了利用三角形三边长求三角形面积的方法,相传这个公式最早是由古希腊数学家阿基米德(公元前 年—公元前
年—公元前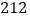 年)得出的,故我国称这个公式为海伦一秦九韶公式.它的表达为:三角形三边长分别为
年)得出的,故我国称这个公式为海伦一秦九韶公式.它的表达为:三角形三边长分别为 、
、 、
、 ,则三角形的面积
,则三角形的面积 (公式里的
(公式里的 为半周长即周长的一半).
为半周长即周长的一半).请利用海伦一秦九韶公式解决以下问题:
(
 )三边长分别为
)三边长分别为 、
、 、
、 的三角形面积为__________.
的三角形面积为__________.(
 )四边形
)四边形 中,
中, ,
, ,
,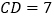 ,
, ,
,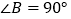 ,四边形
,四边形 的面积为__________.
的面积为__________.(
 )五边形
)五边形 中,
中, ,
, ,
, ,
,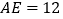 ,
, ,
,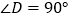 ,五边形
,五边形 的面积为__________.
的面积为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC是一张等腰直角三角形纸板,∠B=90°,AB=BC=1.
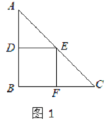
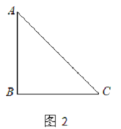
(1)要在这张纸板上剪出一个正方形,使这个正方形的四个顶点都在△ABC的边上.小林设计出了一种剪法,如图1所示.请你再设计出一种不同于图1的剪法,并在图2中画出来.
(2)若按照小林设计的图1所示的剪法来进行裁剪,记图1为第一次裁剪,得到1个正方形,将它的面积记为
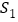 ,则
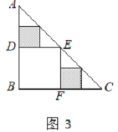
,则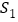 =___________;在余下的2个三角形中还按照小林设计的剪法进行第二次裁剪(如图3),得到2个新的正方形,将此次所得2个正方形的面积的和记为
=___________;在余下的2个三角形中还按照小林设计的剪法进行第二次裁剪(如图3),得到2个新的正方形,将此次所得2个正方形的面积的和记为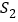 ,则
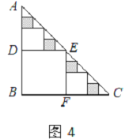
,则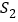 =___________;在余下的4个三角形中再按照小林设计的的剪法进行第三次裁剪(如图4),得到4个新的正方形,将此次所得4个正方形的面积的和记为
=___________;在余下的4个三角形中再按照小林设计的的剪法进行第三次裁剪(如图4),得到4个新的正方形,将此次所得4个正方形的面积的和记为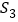 ;按照同样的方法继续操作下去……,第
;按照同样的方法继续操作下去……,第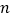 次裁剪得到_________个新的正方形,它们的面积的和
次裁剪得到_________个新的正方形,它们的面积的和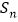 =______________.
=______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在平行四边形ABCD中,AM=CN.求证:四边形MBND是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在所给的网格图中,完成下列各题(用直尺画图,否则不给分)
(1)画出格点△ABC关于直线DE的对称的△A1B1C1;
(2)在DE上画出点P,使PA+PC最小;
(3)在DE上画出点Q,使QA﹣QB最大.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有甲、乙、丙三种糖果混合而成的什锦糖100千克,其中各种糖果的单价和千克数如表所示,商家用加权平均数来确定什锦糖的单价.
甲种糖果
乙种糖果
丙种糖果
单价(元/千克)
15
25
30
千克数
40
40
20
(1)求该什锦糖的单价.
(2)为了使什锦糖的单价每千克至少降低2元,商家计划在什锦糖中加入甲、丙两种糖果共100千克,问其中最多可加入丙种糖果多少千克? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2﹣mx﹣3(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
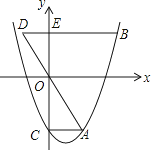
(1)用含m的代数式表示BE的长.
(2)当m=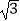 时,判断点D是否落在抛物线上,并说明理由.
时,判断点D是否落在抛物线上,并说明理由.
(3)若AG∥y轴,交OB于点F,交BD于点G.
①若△DOE与△BGF的面积相等,求m的值.
②连结AE,交OB于点M,若△AMF与△BGF的面积相等,则m的值是 .
相关试题

