【题目】已知抛物线l1与l2形状相同,开口方向不同,其中抛物线l1:y=ax2﹣8ax﹣![]() 交x轴于A,B两点(点A在点B的左侧),且AB=6;抛物线l2与l1交于点A和点C(5,n).
交x轴于A,B两点(点A在点B的左侧),且AB=6;抛物线l2与l1交于点A和点C(5,n).
(1)求抛物线l1,l2的表达式;
(2)当x的取值范围是 时,抛物线l1与l2上的点的纵坐标同时随横坐标的增大而增大;
(3)直线MN∥y轴,交x轴,l1,l2分别相交于点P(m,0),M,N,当1≤m≤7时,求线段MN的最大值.
参考答案:
【答案】(1)y=![]() x2﹣2x+
x2﹣2x+![]() (2)2≤x≤4(3)12
(2)2≤x≤4(3)12
【解析】
(1)首先确定A、B两点坐标,求出抛物线l1的解析式,再求出点C坐标,利用待定系数法求出抛物线l2的解析式即可;
(2)观察图象可知,中两个抛物线的顶点之间时,抛物线l1与l2上的点的纵坐标同时随横坐标的增大而增大,求出两个抛物线的顶点坐标即可解决问题;
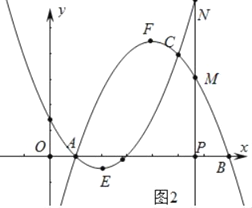
(3)分两种情形分别求解:①如图1中,当1≤m≤5时,MN=﹣m2+6m﹣5=﹣(m﹣3)2+4,②如图2中,当5<m≤7时,MN=m2﹣6m+5=(m﹣3)2﹣4,利用二次函数的性质即可解决问题;
(1)由题意抛物线l1的对称轴x=﹣![]() =4,
=4,
∵抛物线l1交x轴于A,B两点(点A在点B的左侧),且AB=6,
∴A(1,0),B(7,0),
把A(1,0)代入y=ax2﹣8ax﹣![]() ,解得a=﹣
,解得a=﹣![]() ,
,
∴抛物线l1的解析式为y=﹣![]() x2+4x﹣
x2+4x﹣![]() ,
,
把C(5,n)代入y=﹣![]() x2+4x﹣
x2+4x﹣![]() ,解得n=4,
,解得n=4,
∴C(5,4),
∵抛物线l1与l2形状相同,开口方向不同,
∴可以假设抛物线l2的解析式为y=![]() x2+bx+c,
x2+bx+c,
把A(1,0),C(5,4)代入y=![]() x2+bx+c,
x2+bx+c,
得到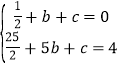 ,解得
,解得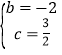 ,
,
∴抛物线l2的解析式为y=![]() x2﹣2x+
x2﹣2x+![]() .
.
(2)观察图象可知,中两个抛物线的顶点之间时,抛物线l1与l2上的点的纵坐标同时随横坐标的增大而增大,
顶点E(2,﹣![]() ),顶点F(4,
),顶点F(4,![]() )
)
所以2≤x≤4时,抛物线l1与l2上的点的纵坐标同时随横坐标的增大而增大,
故答案为2≤x≤4.
(3)∵直线MN∥y轴,交x轴,l1,l2分别相交于点P(m,0),M,N,
∴M(m,﹣![]() m2+4m﹣
m2+4m﹣![]() ),N(m,
),N(m,![]() m2﹣2m+
m2﹣2m+![]() ),
),
①如图1中,当1≤m≤5时,
MN=﹣m2+6m﹣5=﹣(m﹣3)2+4,
∴m=3时,MN的最大值为4.
②如图2中,当5<m≤7时,MN=m2﹣6m+5=(m﹣3)2﹣4,
5<m≤7时,在对称轴右侧,MN随m的增大而增大,
∴m=7时,MN的值最大,最大值是12,
综上所述,MN的最大值为12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A的坐标为(6,0),点B的坐标为(0,8),点C的坐标为(﹣2
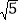 ,4),点M,N分别为四边形OABC边上的动点,动点M从点O开始,以每秒1个单位长度的速度沿O→A→B路线向终点B匀速运动,动点N从O点开始,以每秒两个单位长度的速度沿O→C→B→A路线向终点A匀速运动,点M,N同时从O点出发,当其中一点到达终点后,另一点也随之停止运动,设动点运动的时间t秒(t>0),△OMN的面积为S.
,4),点M,N分别为四边形OABC边上的动点,动点M从点O开始,以每秒1个单位长度的速度沿O→A→B路线向终点B匀速运动,动点N从O点开始,以每秒两个单位长度的速度沿O→C→B→A路线向终点A匀速运动,点M,N同时从O点出发,当其中一点到达终点后,另一点也随之停止运动,设动点运动的时间t秒(t>0),△OMN的面积为S.(1)填空:AB的长是 ,BC的长是 ;
(2)当t=3时,求S的值;
(3)当3<t<6时,设点N的纵坐标为y,求y与t的函数关系式;
(4)若S=
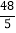 ,请直接写出此时t的值.
,请直接写出此时t的值.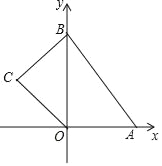
-
科目: 来源: 题型:
查看答案和解析>>【题目】某高校共有5个大餐厅和2个小餐厅。经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐。
(1)1个大餐厅和1个小餐厅分别可供多少名学生就餐?
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,EF⊥AC于F,DB⊥AC于M,∠1=∠2,∠3=∠C.
(1)求证:AB//MN.
(2)若∠C=40°,∠MND=100°,求∠CAD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(探究过程题)用直接开平方法解一元二次方程4(2x﹣1)2﹣25(x+1)2=0.
解:移项得4(2x﹣1)2=25(x+1)2,①
直接开平方得2(2x﹣1)=5(x+1),②
∴x=﹣7. ③
上述解题过程,有无错误如有,错在第_____步,原因是_____,请写出正确的解答过程_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用直接开平方法解下列方程:
(1)(x﹣2)2=3;
(2)2(x﹣3)2=72;
(3)9(y+4)2﹣49=0;
(4)4(2y﹣5)2=9(3y﹣1)2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点A(a,0),B (b,0),a、b满足方程组
 ,C为y轴正半轴上一点,且
,C为y轴正半轴上一点,且 .
.(1)求A、B、C三点的坐标;
(2)是否存在点D(t,-t)使
 ?若存在,请求出D点坐标;若不存在,请说明理由.
?若存在,请求出D点坐标;若不存在,请说明理由.(3)已知E(-2,-4),若坐标轴上存在一点P,使
 ,请求出P的坐标.
,请求出P的坐标.
相关试题

