【题目】在平面直角坐标系中(单位长度为![]() ),已知点
),已知点![]() ,
,![]() ,且
,且![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)若点![]() 是第一象限内一点,且
是第一象限内一点,且![]() 轴,点
轴,点![]() 到
到![]() 轴的距离为4,过点
轴的距离为4,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 从点
从点![]() 处出发,以每秒
处出发,以每秒![]() 的速度沿直线
的速度沿直线![]() 向左移动,点
向左移动,点![]() 从原点
从原点![]() 同时出发,以每秒
同时出发,以每秒![]() 的速度沿
的速度沿![]() 轴向右移动.
轴向右移动.
①经过几秒![]() 平行于
平行于![]() 轴?
轴?
②若某一时刻以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形的面积是
为顶点的四边形的面积是![]() ,求此时点
,求此时点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ,②(4,4)或(
,②(4,4)或(![]() ,4)
,4)
【解析】
(1)利用算术平方根和绝对值的非负性,即可求出答案;
(2)①设t秒后PQ平行于y轴,由于AP∥OQ,所以当AP=OQ时,四边形AOQP是平行四边形,那么PQ平行于y轴,根据AP=OQ列出关于t的方程,解方程即可;
②设t秒后四边形AOQP的面积为10cm2,分两种情况,根据四边形AOQP的面积=![]() (OQ+AP)OA列出关于t的方程,进而求出点P的坐标.
(OQ+AP)OA列出关于t的方程,进而求出点P的坐标.
解:(1)∵![]() ,
,
∴![]() ,
,
解得:![]() ;
;
(2)如图:
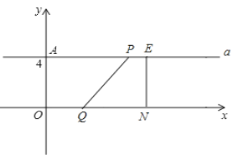
①当AP=QO时,PQ平行于y轴
∴![]() ,
,
解得:![]() ;
;
②分两种情况考虑;
如果P在第一象限
∴![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴AP=![]() ,
,
∴P的坐标(4,4);
如果P在第二象限
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴P的坐标(![]() ,4);
,4);
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中AB=15,AC=13,高AD=12,求BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE平分∠BOD.
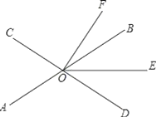
(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.
①用含x的代数式表示∠EOF;
②求∠AOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】七年级(2)班的同学组织到人民公园游玩,张明、王励、李华三位同学和其他同学走散了,同学们已到中心广场,他们三个对着景区示意图在电话中向在中心广场的同学们说他们的位置,张明说他的坐标是
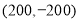 ,王励说他的坐标是
,王励说他的坐标是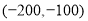 ,李华说他的坐标是
,李华说他的坐标是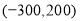 .
.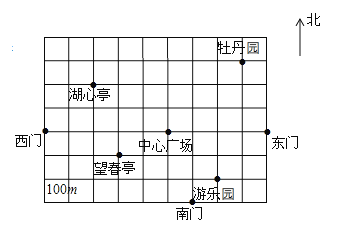
(1)请你根据题目条件,在图中画出平面直角坐标系;
(2)写出这三位同学所在的位置;
(3)写出除了这三位同学所在位置外,图中其余两个景点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
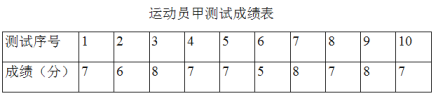
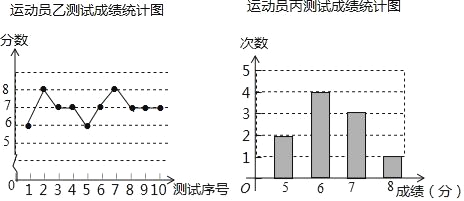
(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、S丙2=0.8)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系xoy中,一次函数y=
 x+3的图象与x轴和y轴交于A、B两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
x+3的图象与x轴和y轴交于A、B两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.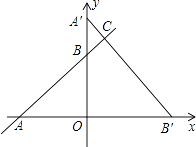
(1)求直线A′B′的解析式;
(2)若直线A′B′与直线AB相交于点C,求S△ABC:S△ABO的值.
相关试题

