【题目】在△ABC中AB=15,AC=13,高AD=12,求BC的长.
参考答案:
【答案】14或4
【解析】
分两种情况讨论:锐角三角形和钝角三角形,根据勾股定理求得BD,CD,再由图形求出BC. 在锐角三角形中,BC=BD+CD,在钝角三角形中,BC=BD-CD.
解:(1)如图,

锐角△ABC中,AC=13,AB=15,BC边上高AD=12,
∵在Rt△ACD中AC=13,AD=12,
∴CD2=AC2-AD2=132-122=25,
∴CD=5,
在Rt△ABD中AB=15,AD=12,由勾股定理得,
BD2=AB2-AD2=152-122=81,
∴BD=9,
∴BC的长为BD+DC=9+5=14,
(2)如图,

钝角△ABC中,AC=13,AB=15,BC边上高AD=12,
在Rt△ACD中AC=13,AD=12,由勾股定理得,
CD2=AC2-AD2=132-122=25,
∴CD=5,
在Rt△ABD中AB=15,AD=12,由勾股定理得,
BD2=AB2-AD2=152-122=81,
∴BD=9,
∴BC的长为DB-BC=9-5=4.
故答案为14或4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了保护环境,某化工厂一期工程完成后购买了3台甲型和2台乙型污水处理设备,共花费资金54万元,且每台乙型设备的价格是每台甲型设备价格的75%.
(1)请你计算每台甲型设备和每台乙型设备的价格各是多少元?
(2)今年该厂二期工程即将完成,产生的污水将大大增加,于是该厂决定再购买甲、乙两种型号设备共8台用于二期工程的污水处理,预算本次购买资金不超过84万元;实际运行中发现,每台甲型设备每月能处理污水200吨,每台乙型设备每月能处理污水160吨,预计二期工程完成后每月将产生不少于1300吨污水,请你求出用于二期工程的污水处理设备的所有购买方案.
(3)经测算:每年用于每台甲型设备的各种维护费和电费为1万元,每年用于每台乙型设备的各种维护费和电费为1.5万元.在(2)中的方案中,哪种购买方案使得设备的各种维护费和电费总费用最低?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,下列推理及括号中所注明的推理依据错误的是( ).
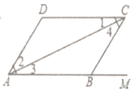
A.∵
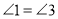 ,∴
,∴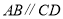 (内错角相等,两直线平行)
(内错角相等,两直线平行)B.∵
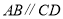 ,∴
,∴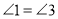 (两直线平行,内错角相等)
(两直线平行,内错角相等)C.∵
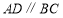 ,∴
,∴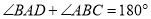 (两直线平行,同旁内角互补)
(两直线平行,同旁内角互补)D.∵
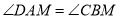 ,∴
,∴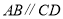 (同位角相等,两直线平行)
(同位角相等,两直线平行) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
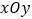 中,定义直线
中,定义直线 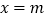 与双曲线
与双曲线 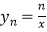 的交点
的交点 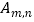 (m、n为正整数)为 “双曲格点”,双曲线
(m、n为正整数)为 “双曲格点”,双曲线 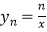 在第一象限内的部分沿着竖直方向平移或以平行于
在第一象限内的部分沿着竖直方向平移或以平行于 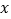 轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.
轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.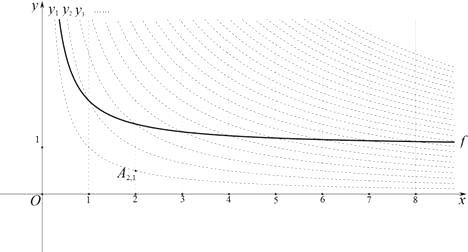
(1)①“双曲格点”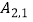 的坐标为;
的坐标为;
②若线段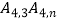 的长为1个单位长度,则n=;
的长为1个单位长度,则n=;
(2)图中的曲线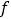 是双曲线
是双曲线 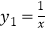 的一条“派生曲线”,且经过点
的一条“派生曲线”,且经过点 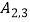 ,则
,则 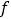 的解析式为 y=;
的解析式为 y=;
(3)画出双曲线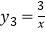 的“派生曲线”g(g与双曲线
的“派生曲线”g(g与双曲线 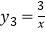 不重合),使其经过“双曲格点”
不重合),使其经过“双曲格点” 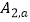 、
、 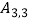 、
、 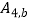 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE平分∠BOD.
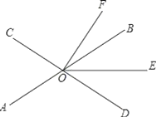
(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.
①用含x的代数式表示∠EOF;
②求∠AOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】七年级(2)班的同学组织到人民公园游玩,张明、王励、李华三位同学和其他同学走散了,同学们已到中心广场,他们三个对着景区示意图在电话中向在中心广场的同学们说他们的位置,张明说他的坐标是
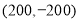 ,王励说他的坐标是
,王励说他的坐标是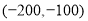 ,李华说他的坐标是
,李华说他的坐标是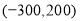 .
.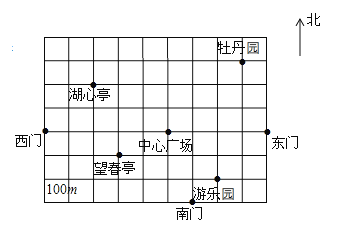
(1)请你根据题目条件,在图中画出平面直角坐标系;
(2)写出这三位同学所在的位置;
(3)写出除了这三位同学所在位置外,图中其余两个景点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中(单位长度为
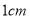 ),已知点
),已知点 ,
,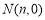 ,且
,且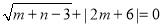 .
.(1)求
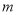 ,
,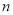 的值;
的值;(2)若点
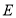 是第一象限内一点,且
是第一象限内一点,且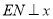 轴,点
轴,点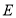 到
到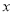 轴的距离为4,过点
轴的距离为4,过点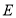 作
作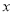 轴的平行线
轴的平行线 ,与
,与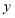 轴交于点
轴交于点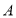 ,点
,点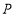 从点
从点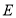 处出发,以每秒
处出发,以每秒 的速度沿直线
的速度沿直线 向左移动,点
向左移动,点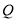 从原点
从原点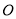 同时出发,以每秒
同时出发,以每秒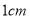 的速度沿
的速度沿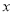 轴向右移动.
轴向右移动.①经过几秒
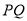 平行于
平行于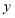 轴?
轴?②若某一时刻以
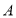 ,
,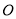 ,
,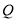 ,
,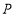 为顶点的四边形的面积是
为顶点的四边形的面积是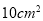 ,求此时点
,求此时点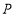 的坐标.
的坐标.
相关试题

