【题目】已知:如图,在平面直角坐标系xoy中,一次函数y= ![]() x+3的图象与x轴和y轴交于A、B两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
x+3的图象与x轴和y轴交于A、B两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.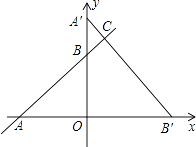
(1)求直线A′B′的解析式;
(2)若直线A′B′与直线AB相交于点C,求S△ABC:S△ABO的值.
参考答案:
【答案】
(1)解:根据y= ![]() x+3,解得点坐标A(﹣4,0),B(0,3),即OA=4,OB=3,
x+3,解得点坐标A(﹣4,0),B(0,3),即OA=4,OB=3,
∴OA′=OA=4,OB′=OB=3,
∴A′(0,4),B′(3,0),
设直线A′B′的解析式为y=kx+b,则 ![]() ,解得
,解得 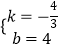 ,
,
∴直线A′B′的解析式为y=﹣ ![]() +4;
+4;
(2)解:解方程组  ,
,
求得两直线交点坐标,得C( ![]() ,
, ![]() ),
),
∴S△A′BC=1× ![]() =
= ![]() ,S△ABO=4×3×
,S△ABO=4×3× ![]() =6,
=6,
∴ ![]() =
= ![]() .
.
【解析】(1)抓住已知将△AOB绕点O顺时针旋转90°后得到△A′OB′.根据旋转的性质得出OA′=OA,OB′=OB,先求出直线AB与两坐标轴的交点坐标,即可得出点A′,B′的坐标,利用待定系数法就可以求出直线A′B′的解析式。
(2)先根据两函数解析式联立方程组,求出方程组的解,即点C的坐标,就可以求出△A′BC和△ABO的面积,即可求出它们的面积之比。
【考点精析】本题主要考查了确定一次函数的表达式和三角形的面积的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;三角形的面积=1/2×底×高才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中(单位长度为
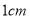 ),已知点
),已知点 ,
,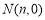 ,且
,且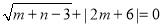 .
.(1)求
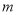 ,
,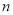 的值;
的值;(2)若点
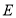 是第一象限内一点,且
是第一象限内一点,且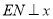 轴,点
轴,点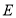 到
到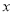 轴的距离为4,过点
轴的距离为4,过点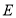 作
作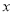 轴的平行线
轴的平行线 ,与
,与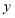 轴交于点
轴交于点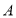 ,点
,点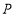 从点
从点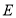 处出发,以每秒
处出发,以每秒 的速度沿直线
的速度沿直线 向左移动,点
向左移动,点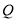 从原点
从原点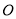 同时出发,以每秒
同时出发,以每秒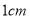 的速度沿
的速度沿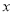 轴向右移动.
轴向右移动.①经过几秒
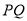 平行于
平行于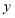 轴?
轴?②若某一时刻以
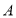 ,
,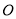 ,
,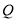 ,
,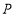 为顶点的四边形的面积是
为顶点的四边形的面积是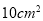 ,求此时点
,求此时点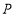 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
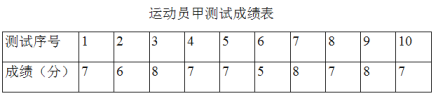
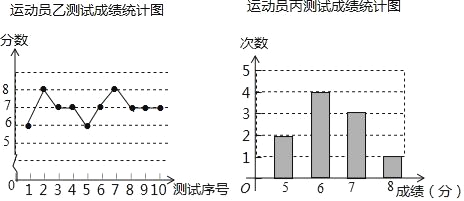
(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、S丙2=0.8)
-
科目: 来源: 题型:
查看答案和解析>>【题目】黄石市在创建国家级文明卫生城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y,图中的折线表示y与x之间的函数关系.
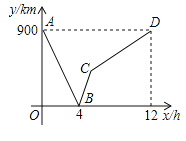
(1)甲、乙两地之间的距离为 千米;图中点B的实际意义是 ;
(2)求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围;
(3)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?
-
科目: 来源: 题型:
查看答案和解析>>【题目】货车在公路A处加满油后,以每小时60千米的速度匀速行驶,前往与A处相距360千米的B处.下表记录的是货车一次加满油后油箱剩余油量y(升)与行驶时间x(时)之间的关系:

(1)如果y关于x的函数是一次函数,求这个函数解析式(不要求写出自变量的取值范围)
(2)在(1)的条件下,如果货车的行驶速度和每小时的耗油量都不变,货车行驶4小时后到达C处,C的前方12千米的D处有一加油站,那么在D处至少加多少升油,才能使货车到达B处卸货后能顺利返回会D处加油?(根据驾驶经验,为保险起见,油箱内剩余油量应随时不少于10升)
相关试题

