【题目】如图,直线AB、CD相交于点O,OE平分∠BOD.
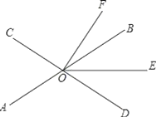
(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.
①用含x的代数式表示∠EOF;
②求∠AOC的度数.
参考答案:
【答案】(1)55°(2)①![]() x②100°
x②100°
【解析】
(1)由对顶角的性质可知∠BOD=70°,从而可求得∠FOB=20°,由角平分线的定义可知∠BOE=![]() ∠BOD,最后根据∠EOF=∠BOE+∠FOB求解即可;
∠BOD,最后根据∠EOF=∠BOE+∠FOB求解即可;
(2)①先证明∠AOE=∠COE= x°,然后由角平分线的定义可知∠FOE=![]() x°;
x°;
②∠BOE=∠FOE-∠FOB可知∠BOE=![]() x°-15°,最后根据∠BOE+∠AOE=180°列出方程可求得x的值,从而可求得∠AOC的度数.
x°-15°,最后根据∠BOE+∠AOE=180°列出方程可求得x的值,从而可求得∠AOC的度数.
解:(1)由对顶角相等可知:∠BOD=∠AOC=70°,
∵∠FOB=∠DOF-∠BOD,
∴∠FOB=90°-70°=20°,
∵OE平分∠BOD,
∴∠BOE=![]() ∠BOD=
∠BOD=![]() ×70°=35°,
×70°=35°,
∴∠EOF=∠FOB+∠BOE=35°+20°=55°;
(2)①∵OE平分∠BOD,
∴∠BOE=∠DOE,
∵∠BOE+∠AOE=180°,∠COE+∠DOE=180°,
∴∠COE=∠AOE=x°,
∵OF平分∠COE,
∴∠EOF=![]() x°;
x°;
②∵∠BOE=∠FOE-∠FOB,
∴∠BOE=![]() x°-15°,
x°-15°,
∵∠BOE+∠AOE=180°,
∴![]() x°-15°+x°=180°,解得:x=130,
x°-15°+x°=180°,解得:x=130,
∴∠AOC=2∠BOE=2×(180°-130°)=100°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,下列推理及括号中所注明的推理依据错误的是( ).
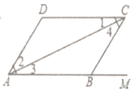
A.∵
 ,∴
,∴ (内错角相等,两直线平行)
(内错角相等,两直线平行)B.∵
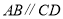 ,∴
,∴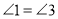 (两直线平行,内错角相等)
(两直线平行,内错角相等)C.∵
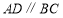 ,∴
,∴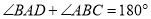 (两直线平行,同旁内角互补)
(两直线平行,同旁内角互补)D.∵
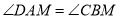 ,∴
,∴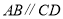 (同位角相等,两直线平行)
(同位角相等,两直线平行) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
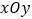 中,定义直线
中,定义直线 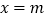 与双曲线
与双曲线 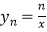 的交点
的交点 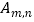 (m、n为正整数)为 “双曲格点”,双曲线
(m、n为正整数)为 “双曲格点”,双曲线 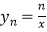 在第一象限内的部分沿着竖直方向平移或以平行于
在第一象限内的部分沿着竖直方向平移或以平行于 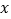 轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.
轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.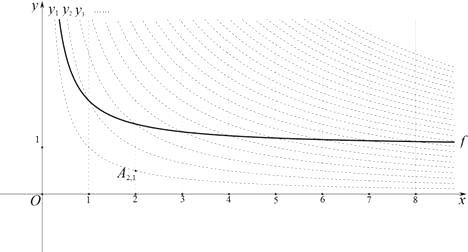
(1)①“双曲格点”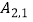 的坐标为;
的坐标为;
②若线段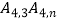 的长为1个单位长度,则n=;
的长为1个单位长度,则n=;
(2)图中的曲线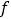 是双曲线
是双曲线 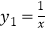 的一条“派生曲线”,且经过点
的一条“派生曲线”,且经过点 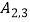 ,则
,则 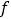 的解析式为 y=;
的解析式为 y=;
(3)画出双曲线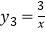 的“派生曲线”g(g与双曲线
的“派生曲线”g(g与双曲线 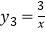 不重合),使其经过“双曲格点”
不重合),使其经过“双曲格点” 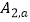 、
、 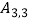 、
、 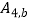 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中AB=15,AC=13,高AD=12,求BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】七年级(2)班的同学组织到人民公园游玩,张明、王励、李华三位同学和其他同学走散了,同学们已到中心广场,他们三个对着景区示意图在电话中向在中心广场的同学们说他们的位置,张明说他的坐标是
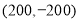 ,王励说他的坐标是
,王励说他的坐标是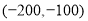 ,李华说他的坐标是
,李华说他的坐标是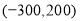 .
.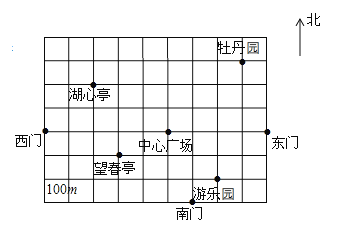
(1)请你根据题目条件,在图中画出平面直角坐标系;
(2)写出这三位同学所在的位置;
(3)写出除了这三位同学所在位置外,图中其余两个景点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中(单位长度为
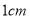 ),已知点
),已知点 ,
,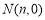 ,且
,且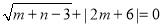 .
.(1)求
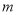 ,
,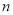 的值;
的值;(2)若点
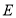 是第一象限内一点,且
是第一象限内一点,且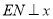 轴,点
轴,点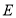 到
到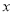 轴的距离为4,过点
轴的距离为4,过点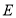 作
作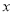 轴的平行线
轴的平行线 ,与
,与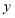 轴交于点
轴交于点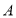 ,点
,点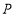 从点
从点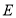 处出发,以每秒
处出发,以每秒 的速度沿直线
的速度沿直线 向左移动,点
向左移动,点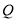 从原点
从原点 同时出发,以每秒
同时出发,以每秒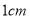 的速度沿
的速度沿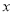 轴向右移动.
轴向右移动.①经过几秒
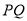 平行于
平行于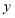 轴?
轴?②若某一时刻以
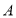 ,
,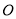 ,
,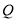 ,
,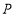 为顶点的四边形的面积是
为顶点的四边形的面积是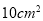 ,求此时点
,求此时点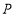 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.

相关试题

