【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=![]() DC,连接EF并延长交BC的延长线于点G.
DC,连接EF并延长交BC的延长线于点G.
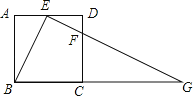
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.
参考答案:
【答案】(1)见解析;(2)10
【解析】
试题分析:(1)利用正方形的性质,可得∠A=∠D,根据已知可得![]() ,根据有两边对应成比例且夹角相等三角形相似,可得△ABE∽△DEF;
,根据有两边对应成比例且夹角相等三角形相似,可得△ABE∽△DEF;
(2)根据平行线分线段成比例定理,可得CG的长,即可求得BG的长.
(1)证明:∵ABCD为正方形,
∴AD=AB=DC=BC,∠A=∠D=90°,
∵AE=ED,
∴![]() ,
,
∵DF=![]() DC,
DC,
∴![]() ,
,
∴![]() ,
,
∴△ABE∽△DEF;
(2)解:∵ABCD为正方形,
∴ED∥BG,
∴![]() ,
,
又∵DF=![]() DC,正方形的边长为4,
DC,正方形的边长为4,
∴ED=2,CG=6,
∴BG=BC+CG=10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列单项式:-x、2x2、-3x3、4x4…-19x19、20x20…根据你发现的规律,第2015个单项式是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
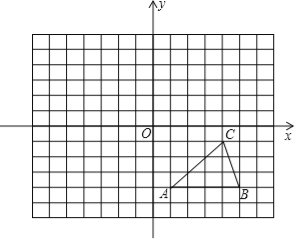
(1)把△ABC向上平移5个单位后得到对应的△A1B1C1,画出△A1B1C1,并写出C1的坐标;
(2)以原点O为对称中心,再画出与△A1B1C1关于原点O对称的△A2B2C2,并写出点C2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠C=90°,AC=3,BC=4,△ABC外接圆⊙O的半径为 ,△ABC内切圆⊙I的半径为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面现象说明“线动成面”的是( )
A. 旋转一扇门,门在空中运动的痕迹 B. 扔一块小石子,石子在空中飞行的路线
C. 天空划过一道流星 D. 汽车雨刷在挡风玻璃上面画出的痕迹
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一个平面截长方体、五棱柱、圆柱和圆锥,不能截出三角形的是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知Rt△ABC,∠ABC=90°,以直角边AB为直径作⊙O,交斜边AC于点D,连接BD.
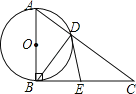
(1)若AD=3,BD=4,求边BC的长;
(2)取BC的中点E,连接ED,试证明ED与⊙O相切.
相关试题

