【题目】如图,已知Rt△ABC,∠ABC=90°,以直角边AB为直径作⊙O,交斜边AC于点D,连接BD.
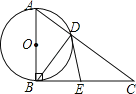
(1)若AD=3,BD=4,求边BC的长;
(2)取BC的中点E,连接ED,试证明ED与⊙O相切.
参考答案:
【答案】(1)BC=![]() ;(2)见解析
;(2)见解析
【解析】
试题分析:(1)根据勾股定理易求AB的长;根据△ABD∽△ACB得比例线段可求BC的长.
(2)连接OD,证明DE⊥OD.
(1)解:∵AB为直径,
∴∠ADB=90°,即BD⊥AC.
在Rt△ADB中,∵AD=3,BD=4,
∴由勾股定理得AB=5.
∵∠ABC=90°,BD⊥AC,
∴△ABD∽△ACB,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
∴BC=![]() ;
;
(2)证明:连接OD,
∵OD=OB,
∴∠ODB=∠OBD;
又∵E是BC的中点,BD⊥AC,
∴DE=BE,
∴∠EDB=∠EBD.
∴∠ODB+∠EDB=∠OBD+∠EBD=90°,
即∠ODE=90°,
∴DE⊥OD.
∴ED与⊙O相切.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=
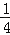 DC,连接EF并延长交BC的延长线于点G.
DC,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面现象说明“线动成面”的是( )
A. 旋转一扇门,门在空中运动的痕迹 B. 扔一块小石子,石子在空中飞行的路线
C. 天空划过一道流星 D. 汽车雨刷在挡风玻璃上面画出的痕迹
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一个平面截长方体、五棱柱、圆柱和圆锥,不能截出三角形的是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形,两条直角边分别为6cm,8cm,斜边长为10cm,若分别以一边旋转一周(①结果用π表示;②你可能用到其中的一个公式,V圆柱=πr2h,V球体=
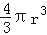 ,V圆锥=
,V圆锥=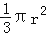 h)
h)(1)如果绕着它的斜边所在的直线旋转一周形成的几何体是?
(2)如果绕着它的直角边6所在的直线旋转一周形成的几何体的体积是多少?
(3)如果绕着它的斜边10所在的直线旋转一周形成的几何体的体积与绕着直角边8所在的直线旋转一周形成的几何体的体积哪个大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)36﹣76+(﹣23)﹣105
(2)
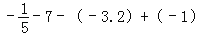
(3)
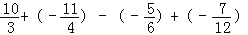
(4)
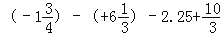
(5)
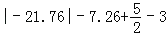
(6)
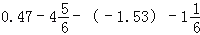 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】杭州休博会期间,嘉年华游乐场投资150万元引进一项大型游乐设施.若不计维修保养费用,预计开放后每月可创收33万元.而该游乐设施开放后,从第1个月到第x个月的维修保养费用累计为y(万元),且y=ax2+bx;若将创收扣除投资和维修保养费用称为游乐场的纯收益g(万元),g也是关于x的二次函数;
(1)若维修保养费用第1个月为2万元,第2个月为4万元.求y关于x的解析式;
(2)求纯收益g关于x的解析式;
(3)问设施开放几个月后,游乐场的纯收益达到最大;几个月后,能收回投资?
相关试题

