【题目】用“☆”定义一种新运算:对于任意有理数a和b,
规定a ☆![]() . 如:1☆
. 如:1☆![]() .
.
(1)求(﹣2)☆5的值;
(2)若![]() ☆3=8,求a的值;
☆3=8,求a的值;
(3)若m=2☆x, n=(-1-x)☆3(其中x为有理数),试比较大小m n(填“>”、“<”或“=”).
参考答案:
【答案】(1)﹣32;(2)a=3;(3)>
【解析】
(1)根据新运算展开,再求出即可;
(2)先根据新运算展开,再解一元一次方程即可;
(3)先根据新运算展开,再求出m、n,即可得出答案.
(1)(-2)☆5=(-2)×52-2×(-2)×5+(-2)=-32;
(2)![]() ☆3=8,
☆3=8,
![]() ×32-2×
×32-2×![]() ×3+
×3+![]() =8,
=8,
9(a+1)-6(a+1)+a+1=16,
9a+9-6a-6+a+1=16,
4a=12,
a=3;
(3)∵m=2☆x=2x2-2×2x+2=2x2-4x+2,n=(![]() -x)☆3=(
-x)☆3=(![]() -x)32-2(
-x)32-2(![]() -x)3+
-x)3+![]() =-3x+1
=-3x+1![]() ,
,
m-n=2x2-x+![]() =2(x-
=2(x-![]() )2+
)2+![]() >0,
>0,
∴m>n,
故答案为:>.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图数轴上A、B、C三点对应的数分别是a、b、7,满足OA=3,BC=1,P为数轴上一动点,点P从A出发,沿数轴正方向以每秒1.5个单位长度的速度匀速运动,点Q从点C出发在射线CA上向点A匀速运动,且P、Q两点同时出发.
(1)求a、b的值
(2)当P运动到线段OB的中点时,点Q运动的位置恰好是线段AB靠近点B的三等分点,求点Q的运动速度
(3)当P、Q两点间的距离是6个单位长度时,求OP的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)3(x+1)=9
(2)

(3)

(4)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是由几个相同的边长为1的小立方块搭成的几何体.
(1)请画出这个几何体的三视图;
(2)根据三视图,这个几何体的表面积为 个平方单位(包括底面积);
(3)若上述小立方块搭成的几何体的俯视图不变,各位置的小立方块个数可以改变(总数目不变),则搭成的几何体的表面积最大为 个平方单位(包括底面积) .


-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形
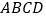 中,
中,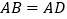 ,
,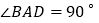 ,
,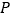 是
是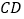 边上一点,连接
边上一点,连接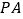 ,过点
,过点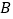 ,
,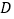 作
作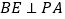 ,
,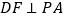 ,垂足分别为
,垂足分别为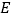 ,
,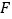 ,如图1.
,如图1.(1)请探究
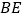 ,
,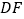 ,
,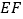 这三条线段有怎样的数量关系?请说明理由;
这三条线段有怎样的数量关系?请说明理由;(2)若点
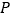 在
在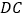 的延长线上,如图2,那么这三条线段的数量关系是 (直接写结果)
的延长线上,如图2,那么这三条线段的数量关系是 (直接写结果)(3)若点
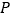 在
在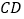 的延长线上,如图3,那么这三条线段的数量关系是 (直接写结果)
的延长线上,如图3,那么这三条线段的数量关系是 (直接写结果)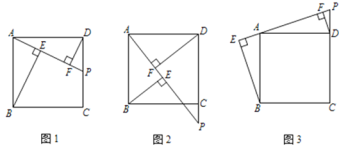
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蔬菜经营户从蔬菜批发市场批发蔬菜进行零售,部分蔬菜批发价格与零售价格如表:
蔬菜品种
西红柿
青椒
西兰花
豆角
批发价(元/kg)
3.6
5.4
8
4.8
零售价(元/吨)
5.4
8.4
14
7.6
请解答下列问题:
(1)第一天,该经营户批发西红柿和西兰花两种蔬菜共300 kg,用去了1520元钱,这两种蔬菜当天全部售完一共能赚多少元钱?
(2)第二天,该经营户用1520元钱仍然批发西红柿和西兰花,要想当天全部售完后赚钱数1050元,则该经营户批发西红柿多少千克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.
(1)求每张门票的原定票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠政策,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率
相关试题

