【题目】计算:|﹣ ![]() |+
|+ ![]() sin45°﹣(
sin45°﹣( ![]() )﹣1﹣
)﹣1﹣ ![]() (π﹣3)0 .
(π﹣3)0 .
参考答案:
【答案】解:原式= ![]() +
+ ![]() ×
× ![]() ﹣3﹣2
﹣3﹣2 ![]() =﹣2﹣
=﹣2﹣ ![]()
【解析】原式第一项利用绝对值的代数意义化简,第二项利用特殊角的三角函数值计算,第三项利用负整数指数幂法则计算,最后一项利用零指数幂法则计算即可得到结果.
【考点精析】本题主要考查了零指数幂法则和整数指数幂的运算性质的相关知识点,需要掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数)才能正确解答此题.
-
科目: 来源: 题型:
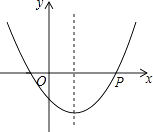
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,若点P(4,0)在该抛物线上,则一元二次方程ax2+bx+c=0的两根为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a,
∵S四边形ADCB=S△ACD+S△ABC= 12 b2+ 12 ab.
又∵S四边形ADCB=S△ADB+S△DCB= 12 c2+ 12 a(b﹣a)
∴ 12 b2+ 12 ab= 12 c2+ 12 a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2 .

-
科目: 来源: 题型:
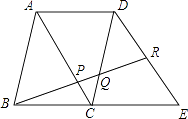
查看答案和解析>>【题目】如图,四边形ABCD和四边形ACED都是平行四边形,点R在DE上,且DR:RE=5:4,BR分别与AC,CD相交于点P,Q,则BP:PQ:QR= .
-
科目: 来源: 题型:
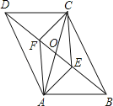
查看答案和解析>>【题目】如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是( )
A.4 B.3 C.2 D.1
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了增强公民的节水意识,合理利用水资源,某市采用价格调控手段来引导市民节约用水:每户居民每月用水不超过15立方米时,按基本价格x元/立方米进行收费;超过15立方米时,加价收费,超过的部分按y元/立方米收费.该市某户居民今年3、4、5月份的用水量和水费如下表所示:
月份
用水量(立方米)
水费(元)
3
16
50
4
20
70
5
m
不低于36元且不超过95元
(1)求x、y的值;
(2)求该居民5月份用水量m的范围.
-
科目: 来源: 题型:
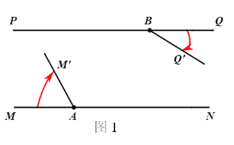
查看答案和解析>>【题目】如图1,直线MN//直线PQ,点A、B分别是直线MN、PQ上的两点.将射线AM绕点A顺时针匀速旋转,射线BQ绕点B顺时针匀速旋转,旋转后的射线分别记为AM′、BQ′,已知射线AM、射线BQ旋转的速度之和为7度/秒.
(1)如果射线BQ 先转动30°后,射线AM、BQ′再同时旋转10秒时,射线AM′与BQ′第一次出现平行.求射线AM、BQ的旋转速度;
(2)若射线AM、BQ分别以(1)中速度同时转动t秒,在射线AM′与AN重合之前,求t为何值时AM′⊥BQ′;
(3)若∠BAN=45°,射线AM、BQ分别以(1)中的速度同时转动t秒,在射线AM′与AN重合之前,射线AM′与BQ′交于点H,过点H作HC⊥PQ,垂足为C,如图2所示,设∠BAH=α,∠BHC=β,求α和β满足的数量关系,直接写出结果.


相关试题

