【题目】为了增强公民的节水意识,合理利用水资源,某市采用价格调控手段来引导市民节约用水:每户居民每月用水不超过15立方米时,按基本价格x元/立方米进行收费;超过15立方米时,加价收费,超过的部分按y元/立方米收费.该市某户居民今年3、4、5月份的用水量和水费如下表所示:
月份 | 用水量(立方米) | 水费(元) |
3 | 16 | 50 |
4 | 20 | 70 |
5 | m | 不低于36元且不超过95元 |
(1)求x、y的值;
(2)求该居民5月份用水量m的范围.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】(1)分两种情况:当x≤15时;当x>15时,求得用户用水为x立方米时的水费,列出方程组求解即可;
(2)根据所交水费,列出不等式组求解即可.
(1)设基本水费价格为:x元/立方米,超过的部分的水费价格为:y元/立方米,
根据题意得,
![]() ,
,
解这个方程组得![]() ,
,
答:该市居民用水的基本价格为3元/立方米,超过15立方米部分的价格为5元/立方米.
(2)根据题意得![]() ,
,
解之得![]() ,
,
∴该居民5月份用水量m的范围是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD和四边形ACED都是平行四边形,点R在DE上,且DR:RE=5:4,BR分别与AC,CD相交于点P,Q,则BP:PQ:QR= .
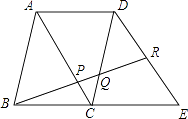
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|﹣
 |+
|+  sin45°﹣(
sin45°﹣(  )﹣1﹣
)﹣1﹣  (π﹣3)0 .
(π﹣3)0 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是( )
A.4 B.3 C.2 D.1
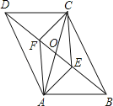
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线MN//直线PQ,点A、B分别是直线MN、PQ上的两点.将射线AM绕点A顺时针匀速旋转,射线BQ绕点B顺时针匀速旋转,旋转后的射线分别记为AM′、BQ′,已知射线AM、射线BQ旋转的速度之和为7度/秒.
(1)如果射线BQ 先转动30°后,射线AM、BQ′再同时旋转10秒时,射线AM′与BQ′第一次出现平行.求射线AM、BQ的旋转速度;
(2)若射线AM、BQ分别以(1)中速度同时转动t秒,在射线AM′与AN重合之前,求t为何值时AM′⊥BQ′;
(3)若∠BAN=45°,射线AM、BQ分别以(1)中的速度同时转动t秒,在射线AM′与AN重合之前,射线AM′与BQ′交于点H,过点H作HC⊥PQ,垂足为C,如图2所示,设∠BAH=α,∠BHC=β,求α和β满足的数量关系,直接写出结果.
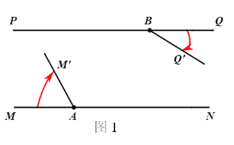


-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD中,AB=BC,∠ABC=120°,∠MBN=60°,∠MBN绕B点旋转,它的两边分别交AD,DC(或它们的延长线)于E,F.
当∠MBN绕B点旋转到AE=CF时(如图1),易证AE+CF=EF;
当∠MBN绕B点旋转到AE≠CF时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,线段AE,CF,EF又有怎样的数量关系?请写出你的猜想,不需证明.
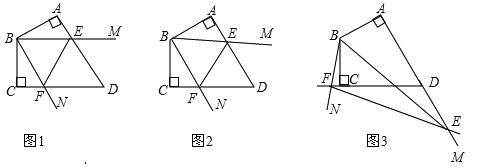
-
科目: 来源: 题型:
查看答案和解析>>【题目】潜山市某村办工厂,今年前5个月生产某种产品的总量C(件)关于时间t(月)的函数图象如图所示,则该厂对这种产品来说( )

A. 1月至3月每月生产总量逐月增加,4、5两月每月生产总量逐月减少
B. 1月至3月每月生产总量逐月增加,4,5两月每月生产量与3月持平
C. 1月至3月每月生产总量逐月增加,4、5两月均停止生产
D. 1月至3月每月生产总量不变,4、5两月均停止生产
相关试题

