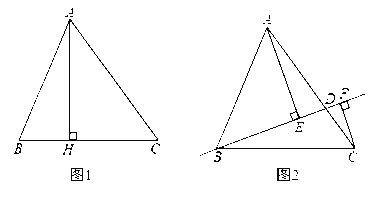
【题目】如图1和2,在△ABC中,AB=13,BC=14,BH=5.
探究:如图1,AH⊥BC于点H,则AH= ,AC= ,△ABC的面积![]() ;
;
拓展:如图2,点D在AC上(可与点A,C重合),分别过点A.C作直线BD的垂线,垂足为E,F,设BD=x,AE=m,CF=n(当点D与点A重合时,我们认为![]() )
)
(1)用含x,m,n的代数式表示![]() 及
及![]() ;
;
(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;
(3)对给定的一个x值,有时只能确定唯一的点D,直接写出这样的x的取值范围.
参考答案:
【答案】探究:12;15;84;拓展:(1)![]() =
=![]() mx;
mx;![]() =
=![]() nx;(2)m+n=
nx;(2)m+n=![]() ;m+n有最大值15;m+n的最小值为12;(3) 11.2.
;m+n有最大值15;m+n的最小值为12;(3) 11.2.
【解析】试题分析:探究:根据勾股定理计算即可;
拓展:(1)根据三角形的面积公式计算;
(2)根据△ABC的面积是84,列出关系式,求出(m+n)与x的函数关系式,结合图形求出(m+n)的最大值和最小值;
(3)根据当BD⊥AC时,m+n有最大值解答.
试题解析:探究:由勾股定理得,AH=![]() =12,
=12,
AC=![]() =15,
=15,
△ABC的面积S△ABC=![]() ×BC×AH=84.
×BC×AH=84.
故答案为:12;15;84;
拓展:(1)![]() =
=![]() ×BD×AE=
×BD×AE=![]() mx,
mx,
![]() =
=![]() ×BD×CH=
×BD×CH=![]() nx;
nx;
(2)![]() mx+
mx+![]() nx=84,
nx=84,
m+n=![]() ,
,
当BD⊥AC时,m+n有最大值15,
当BD值最大时,m+n有最小值.
∴当点D与点C重合时m+n有最小值.
∴m+n的最小值为![]() =12;
=12;
(3)当BD⊥AC时,
x=BD=![]() =11.2,只能确定唯一的点D.
=11.2,只能确定唯一的点D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=9,AD=4. E为CD边上一点,CE=6. 点P从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为t秒.
⑴求AE的长;
⑵当t为何值时,△PAE为直角三角形?
⑶是否存在这样的t,使EA恰好平分∠PED,若存在,求出t的值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】正多边形的每个内角都;若一个正多边形的一个内角是108°,则这个多边形的边数是.
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“全等三角形的周长相等”的逆命题是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现定义两种运算“⊕”和“※”.对于任意两个整数a、b,
都有:a⊕b=a+b﹣1,a※b=ab+2.
(1)分别求出 -3⊕2 的值和 4 ※(-1)的值;
(2)试求(-3⊕2)※ [4 ※(-1)]的值.
-
科目: 来源: 题型:
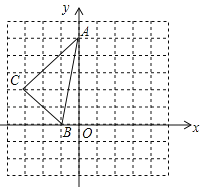
查看答案和解析>>【题目】如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
(1)画出将△ABC向右平移2个单位得到△A1B1C1;
(2)画出将△ABC绕点O顺时针方向旋转90°得到的△A2B2C2;
(3)求△A1B1C1与△A2B2C2重合部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】美丽的丹东吸引了许多外商投资,某外商向丹东连续投资3年,2010年初投资2亿元,2012年初投资3亿元.设每年投资的平
均增长率为x,则列出关于x的方程为 .
相关试题

