【题目】如图,矩形ABCD中,AB=9,AD=4. E为CD边上一点,CE=6. 点P从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为t秒.
⑴求AE的长;
⑵当t为何值时,△PAE为直角三角形?
⑶是否存在这样的t,使EA恰好平分∠PED,若存在,求出t的值;若不存在,请说明理由.

参考答案:
【答案】(1)5;(2)6或![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)在直角△ADE中,利用勾股定理进行解答;
(2)需要分类讨论:AE为斜边和AP为斜边两种情况下的直角三角形;
(3)假设存在.利用角平分线的性质,平行线的性质以及等量代换推知:∠PEA=∠EAP,则PE=PA,由此列出关于t的方程,通过解方程求得相应的t的值即可.
试题解析:(1)∵矩形ABCD中,AB=9,AD=4,
∴CD=AB=9,∠D=90°,
∴DE=9﹣6=3,
∴AE=![]() =5;
=5;
(2)①若∠EPA=90°,t=6;
②若∠PEA=90°,![]() ,
,
解得t=![]() .
.
综上所述,当t=6或t=![]() 时,△PAE为直角三角形;
时,△PAE为直角三角形;
(3)假设存在.
∵EA平分∠PED,
∴∠PEA=∠DEA.
∵CD∥AB,
∴∠DEA=∠EAP,
∴∠PEA=∠EAP,
∴PE=PA,
∴![]() ,
,
解得t=![]() .
.
∴满足条件的t存在,此时t=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a2=25,|b|=3,则a+b的值是( )
A.﹣8
B.±8
C.±2
D.±8或±2 -
科目: 来源: 题型:
查看答案和解析>>【题目】一般地,从n边形的一个顶点出发,可以作(n-3)条对角线,它们将n边形分为个三角形,因此n边形的内角和是个三角形的内角的和,即n边形的内角和等于.
-
科目: 来源: 题型:
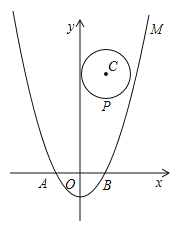
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,将二次函数
 的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N.
的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N.(1)求N的函数表达式;
(2)设点P(m,n)是以点C(1,4)为圆心、1为半径的圆上一动点,二次函数的图象M与x轴相交于两点A、B,求
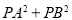 的最大值;
的最大值;(3)若一个点的横坐标与纵坐标均为整数,则该点称为整点.求M与N所围成封闭图形内(包括边界)整点的个数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正多边形的每个内角都;若一个正多边形的一个内角是108°,则这个多边形的边数是.
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“全等三角形的周长相等”的逆命题是_____.
-
科目: 来源: 题型:
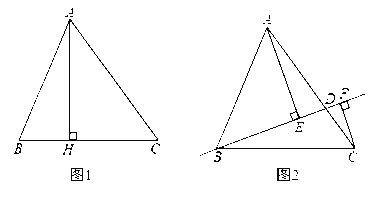
查看答案和解析>>【题目】如图1和2,在△ABC中,AB=13,BC=14,BH=5.
探究:如图1,AH⊥BC于点H,则AH= ,AC= ,△ABC的面积
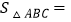 ;
;拓展:如图2,点D在AC上(可与点A,C重合),分别过点A.C作直线BD的垂线,垂足为E,F,设BD=x,AE=m,CF=n(当点D与点A重合时,我们认为
 )
)(1)用含x,m,n的代数式表示
 及
及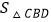 ;
;(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;
(3)对给定的一个x值,有时只能确定唯一的点D,直接写出这样的x的取值范围.
相关试题

