【题目】【问题引入】 已知:如图BE、CF是△ABC的中线,BE、CF相交于G.求证: ![]() =
= ![]() =
= ![]()

证明:连结EF
∵E、F分别是AC、AB的中点
∴EF∥BC且EF= ![]() BC
BC
∴ ![]() =
= ![]() =
= ![]() =
= ![]()
【思考解答】
(1)连结AG并延长AG交BC于H,点H是否为BC中点(填“是”或“不是”)
(2)①如果M、N分别是GB、GC的中点,则四边形EFMN 是四边形. ②当 ![]() 的值为时,四边形EFMN 是矩形.
的值为时,四边形EFMN 是矩形.
③当 ![]() 的值为时,四边形EFMN 是菱形.
的值为时,四边形EFMN 是菱形.
④如果AB=AC,且AB=10,BC=16,则四边形EFMN的面积S= .
参考答案:
【答案】
(1)是
(2)平行;1;![]() ;16
;16
【解析】解:(1)如图,连结EF,交AG于O, 
∵E、F分别是AC、AB的中点,
∴EF是△ABC的中位线,
∴EF∥BC且EF= ![]() BC,
BC,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∵OE∥BH,
∴ ![]() =
= ![]() =
= ![]() ,
,
∵OE∥CH,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴BH=CH,即点H是BC中点;
所以答案是:是;
·(2)①∵M、N分别是GB、GC的中点,
∴MN是△GBC的中位线,
∴MN∥BC且MN= ![]() BC,
BC,
由(1)可得,EF∥BC且EF= ![]() BC,
BC,
∴EF∥MN,EF=MN,
∴四边形EFMN是平行四边形,
所以答案是:平行;
②当四边形EFMN是矩形时,FG=EG,
∵ ![]() =
= ![]() =
= ![]() ,
,
∴GB=GC,
∴∠GBC=∠GCB,
又∵H是BC的中点,
∴GH⊥BC,即AH⊥BC,
∴AH垂直平分BC,
∴AB=AC,
∴ ![]() 的值为1,
的值为1,
所以答案是:1;
③当四边形EFMN是菱形时,MN=FM,
∵MN是△BCG的中位线,
∴MN= ![]() BC,
BC,
∵FM是△ABG的中位线,
∴FM= ![]() AG,
AG,
又∵G是△ABC的重心,
∴AG= ![]() AH,
AH,
∴FM= ![]() AG=
AG= ![]() AH,
AH,
∴ ![]() BC=
BC= ![]() AH,即2BC=3AH,
AH,即2BC=3AH,
∴ ![]() 的值为
的值为 ![]() ,
,
所以答案是: ![]() ;
;
④当AB=AC时,由②可得四边形EFMN是矩形,AH⊥BC,
∵AB=10,BC=16,
∴BH= ![]() BC=8,AH=6,
BC=8,AH=6,
∵MN是△BCG的中位线,
∴MN= ![]() BC=8,
BC=8,
∵FM是△ABG的中位线,
∴FM= ![]() AG=
AG= ![]() AH=2,
AH=2,
∴矩形EFMN的面积S=FM×MN=2×8=16,
所以答案是:16.
【考点精析】掌握三角形中位线定理和平行线分线段成比例是解答本题的根本,需要知道连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;三条平行线截两条直线,所得的对应线段成比例.
-
科目: 来源: 题型:
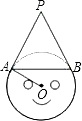
查看答案和解析>>【题目】如图是不倒翁的正视图,不倒翁的圆形脸恰好与帽子边沿PA、PB分别相切于点A、B,不倒翁的鼻尖正好是圆心O,若∠OAB=25°,求∠APB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】哈市某中学为了解学生的课余生活情况,学校决定围绕“在欣赏音乐、读课外书、体育运动.其他活动中,你最喜欢的课余生活种类是什么?(只写一类)”的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查问卷适当整理后绘制成如图所示的不完整的条形统计图,其中最喜欢欣赏音乐的学生占被抽取人数的12%,请你根据以上信息解答下列问题:

(1)在这次调查中,一共抽取了多少名学生?
(2)最喜欢读课外书的学生占被抽取人数的百分数是多少?
(3)如果全校有1000名学生,请你估计全校最喜欢体育运动的学生约有多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】张师傅驾车运送荔枝到某地出售,汽车出发前油箱有油50升,行驶若干小时后,图中在加油站加油若干升,油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.
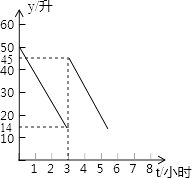
(1)汽车行驶小时后加油,中途加油升;
(2)求加油前油箱剩余油量y与行驶时间t的函数关系式;
(3)已知加油前、后汽车都以70千米/小时匀速行驶,如果加油站距目的地210千米,要到达目的地,问油箱中的油是否够用?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,把矩形OCBA放置于直角坐标系中,OC=3,BC=2,取AB的中点M,连接MC,把△MBC沿x轴的负方向平移OC的长度后得到△DAO.
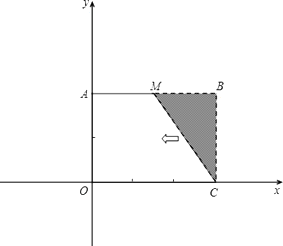
(1)试直接写出点D的坐标;
(2)已知点B与点D在经过原点的抛物线上,点P在第一象限内的该抛物线上移动,过点P作PQ⊥x轴于点Q,连接OP.
①若以O、P、Q为顶点的三角形与△DAO相似,试求出点P的坐标;
②试问在抛物线的对称轴上是否存在一点T,使得|TO﹣TB|的值最大? -
科目: 来源: 题型:
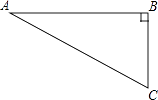
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
A.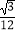
B.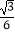
C.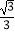
D.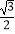
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ABC=90°,AB=BC=2
 ,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( )
,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( ) 
A.2
B.
C.
D.3
相关试题

