【题目】如图,在四边形ABCD中,∠ABC=90°,AB=BC=2 ![]() ,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( )
,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( ) 
A.2
B.![]()
C.![]()
D.3
参考答案:
【答案】C
【解析】解:连接AC,过B作EF的垂线交AC于点G,交EF于点H, 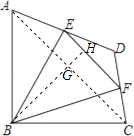
∵∠ABC=90°,AB=BC=2 ![]() ,
,
∴AC= ![]() =
= ![]() =4,
=4,
∵△ABC为等腰三角形,BH⊥AC,
∴△ABG,△BCG为等腰直角三角形,
∴AG=BG=2
∵S△ABC= ![]() ABAC=
ABAC= ![]() ×2
×2 ![]() ×2
×2 ![]() =4,
=4,
∴S△ADC=2,
∵ ![]() =2,
=2,
∴GH= ![]() BG=
BG= ![]() ,
,
∴BH= ![]() ,
,
又∵EF= ![]() AC=2,
AC=2,
∴S△BEF= ![]() EFBH=
EFBH= ![]() ×2×
×2× ![]() =
= ![]() ,
,
故选C.
【考点精析】通过灵活运用三角形的面积,掌握三角形的面积=1/2×底×高即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题引入】 已知:如图BE、CF是△ABC的中线,BE、CF相交于G.求证:
 =
=  =
= 

证明:连结EF
∵E、F分别是AC、AB的中点
∴EF∥BC且EF= BC
BC
∴ =
=  =
=  =
= 
【思考解答】
(1)连结AG并延长AG交BC于H,点H是否为BC中点(填“是”或“不是”)
(2)①如果M、N分别是GB、GC的中点,则四边形EFMN 是四边形. ②当 的值为时,四边形EFMN 是矩形.
的值为时,四边形EFMN 是矩形.
③当 的值为时,四边形EFMN 是菱形.
的值为时,四边形EFMN 是菱形.
④如果AB=AC,且AB=10,BC=16,则四边形EFMN的面积S= . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,把矩形OCBA放置于直角坐标系中,OC=3,BC=2,取AB的中点M,连接MC,把△MBC沿x轴的负方向平移OC的长度后得到△DAO.
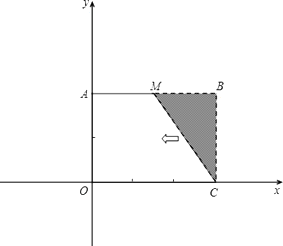
(1)试直接写出点D的坐标;
(2)已知点B与点D在经过原点的抛物线上,点P在第一象限内的该抛物线上移动,过点P作PQ⊥x轴于点Q,连接OP.
①若以O、P、Q为顶点的三角形与△DAO相似,试求出点P的坐标;
②试问在抛物线的对称轴上是否存在一点T,使得|TO﹣TB|的值最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
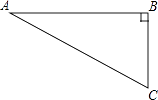
A.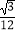
B.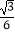
C.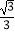
D.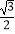
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点F在边AC上,并且CF=1,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是 .
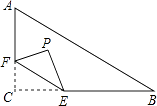
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题:
(1)﹣|﹣1|+ cos30°﹣(﹣
cos30°﹣(﹣  )﹣2+(π﹣3.14)0 .
)﹣2+(π﹣3.14)0 .
(2)(x﹣y)2﹣(x﹣2y)(x+y) -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程与不等式
(1)解方程:x2+3x﹣2=0;
(2)解不等式组: .
.
相关试题

