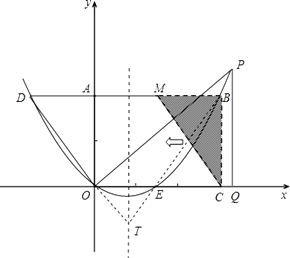
【题目】已知:如图,把矩形OCBA放置于直角坐标系中,OC=3,BC=2,取AB的中点M,连接MC,把△MBC沿x轴的负方向平移OC的长度后得到△DAO.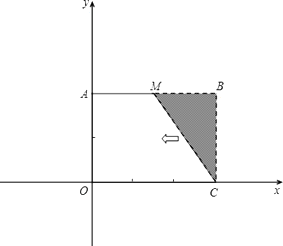
(1)试直接写出点D的坐标;
(2)已知点B与点D在经过原点的抛物线上,点P在第一象限内的该抛物线上移动,过点P作PQ⊥x轴于点Q,连接OP.
①若以O、P、Q为顶点的三角形与△DAO相似,试求出点P的坐标;
②试问在抛物线的对称轴上是否存在一点T,使得|TO﹣TB|的值最大?
参考答案:
【答案】
(1)
解:依题意得:D(﹣ ![]() ,2);
,2);
(2)
解:①∵OC=3,BC=2,
∴B(3,2);
∵抛物线经过原点,
∴设抛物线的解析式为y=ax2+bx (a≠0)
又抛物线经过点B(3,2)与点D(﹣ ![]() ,2);
,2);
∴ 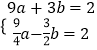
解得: 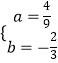
∴抛物线的解析式为y= ![]() ;
;
∵点P在抛物线上,
∴设点P(x, ![]() );
);
1)、若△PQO∽△DAO,则 ![]() ,
,  ,
,
解得:x1=0(舍去)或x2= ![]() ,
,
∴点P( ![]() );
);
2)、若△OQP∽△DAO,则 ![]() ,
, 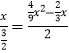 ,
,
解得:x1=0(舍去)或x2= ![]() ,
,
∴点P( ![]() ,6);
,6);
②存在点T,使得|TO﹣TB|的值最大.
抛物线y= ![]() 的对称轴为直线x=
的对称轴为直线x= ![]() ,设抛物线与x轴的另一个交点为E,则点E(
,设抛物线与x轴的另一个交点为E,则点E( ![]() ,0);
,0);
∵点O、点E关于直线x= ![]() 对称,
对称,
∴TO=TE
要使得|TO﹣TB|的值最大,
即是使得|TE﹣TB|的值最大,
根据三角形两边之差小于第三边可知,当T、E、B三点在同一直线上时,|TE﹣TB|的值最大;
设过B、E两点的直线解析式为y=kx+b(k≠0),
∴ 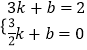
解得: 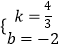
∴直线BE的解析式为y= ![]() x﹣2;
x﹣2;
当x= ![]() 时,y=
时,y= ![]()
∴存在一点T( ![]() ,﹣1)使得|TO﹣TB|最大.
,﹣1)使得|TO﹣TB|最大.
【解析】(1)由于M是AB的中点,即可得到AM= ![]() ,由此可求出M点的坐标,将M点坐标向左平移3个单位即可得到点D的坐标;(2)①根据B、D的坐标即可确定抛物线的解析式,设出P点的横坐标,根据抛物线的解析式可得到P点纵坐标的表达式;由于∠PQO=∠DAO=90°,若以O、P、Q为顶点的三角形与△DAO相似,则有两种情况:1)、△PQO∽△DOA,2)、△OQP∽△DAO;根据上述两种情况所得的不同比例线段,即可求出P点的坐标;②由于D、B关于抛物线的对称轴对称,若|TO﹣TB|的值最大,那么T点必为直线DO与抛物线对称轴的交点,根据抛物线的解析式可求出其对称轴方程,根据D点的坐标可求得直线DO的解析式,联立两个函数的解析式,即可求得T点的坐标.
,由此可求出M点的坐标,将M点坐标向左平移3个单位即可得到点D的坐标;(2)①根据B、D的坐标即可确定抛物线的解析式,设出P点的横坐标,根据抛物线的解析式可得到P点纵坐标的表达式;由于∠PQO=∠DAO=90°,若以O、P、Q为顶点的三角形与△DAO相似,则有两种情况:1)、△PQO∽△DOA,2)、△OQP∽△DAO;根据上述两种情况所得的不同比例线段,即可求出P点的坐标;②由于D、B关于抛物线的对称轴对称,若|TO﹣TB|的值最大,那么T点必为直线DO与抛物线对称轴的交点,根据抛物线的解析式可求出其对称轴方程,根据D点的坐标可求得直线DO的解析式,联立两个函数的解析式,即可求得T点的坐标.
【考点精析】根据题目的已知条件,利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】哈市某中学为了解学生的课余生活情况,学校决定围绕“在欣赏音乐、读课外书、体育运动.其他活动中,你最喜欢的课余生活种类是什么?(只写一类)”的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查问卷适当整理后绘制成如图所示的不完整的条形统计图,其中最喜欢欣赏音乐的学生占被抽取人数的12%,请你根据以上信息解答下列问题:

(1)在这次调查中,一共抽取了多少名学生?
(2)最喜欢读课外书的学生占被抽取人数的百分数是多少?
(3)如果全校有1000名学生,请你估计全校最喜欢体育运动的学生约有多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】张师傅驾车运送荔枝到某地出售,汽车出发前油箱有油50升,行驶若干小时后,图中在加油站加油若干升,油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.
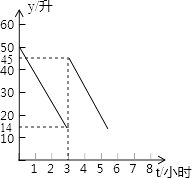
(1)汽车行驶小时后加油,中途加油升;
(2)求加油前油箱剩余油量y与行驶时间t的函数关系式;
(3)已知加油前、后汽车都以70千米/小时匀速行驶,如果加油站距目的地210千米,要到达目的地,问油箱中的油是否够用?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】【问题引入】 已知:如图BE、CF是△ABC的中线,BE、CF相交于G.求证:
 =
=  =
= 

证明:连结EF
∵E、F分别是AC、AB的中点
∴EF∥BC且EF= BC
BC
∴ =
=  =
=  =
= 
【思考解答】
(1)连结AG并延长AG交BC于H,点H是否为BC中点(填“是”或“不是”)
(2)①如果M、N分别是GB、GC的中点,则四边形EFMN 是四边形. ②当 的值为时,四边形EFMN 是矩形.
的值为时,四边形EFMN 是矩形.
③当 的值为时,四边形EFMN 是菱形.
的值为时,四边形EFMN 是菱形.
④如果AB=AC,且AB=10,BC=16,则四边形EFMN的面积S= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
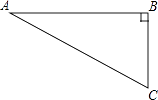
A.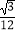
B.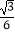
C.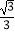
D.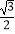
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ABC=90°,AB=BC=2
 ,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( )
,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( ) 
A.2
B.
C.
D.3 -
科目: 来源: 题型:
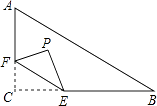
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点F在边AC上,并且CF=1,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是 .
相关试题

