【题目】如图,已知直线![]() ,直线
,直线![]() 交
交![]() 于
于![]() 点,交
点,交![]() 于
于![]() 点,
点,![]() 是线段
是线段![]() 上的一个动点,
上的一个动点,
(1)若![]() 点在线段
点在线段![]() (
(![]() 、
、![]() 两点除外)上运动,问
两点除外)上运动,问![]() ,
,![]() ,
,![]() 之间的关系是什么?这种关系是否变化?
之间的关系是什么?这种关系是否变化?
(2)若![]() 点在线段
点在线段![]() 之外时,
之外时,![]() ,
,![]() ,
,![]() 之间的关系怎样?说明理由
之间的关系怎样?说明理由
参考答案:
【答案】(1)∠APB=∠PAC +∠PBD,不会变化;(2)∠PBD=∠PAC+∠APB或∠PAC=∠PBD+∠APB,理由见解析.
【解析】
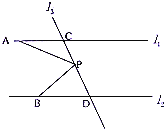
(1)当P点在C、D之间运动时,首先过点P作PE∥l1,由l1∥l2,可得PE∥l2∥l1,根据两直线平行,内错角相等,即可求得:∠APB=∠PAC+∠PBD,即∠APB、∠PAC、∠PBD之间的关系不发生变化;
(2)当点P在C、D两点的外侧运动时,由直线l1∥l2,根据两直线平行,同位角相等以及三角形外角的性质,即可求得∠PAC,∠APB,∠PBD之间的关系.
(1)如图①,当P点在C、D之间运动时,∠APB=∠PAC+∠PBD.
理由如下:过点P作PE∥l1,

∵l1∥l2,
∴PE∥l2∥l1,
∴∠PAC=∠1,∠PBD=∠2,
∴∠APB=∠1+∠2=∠PAC+∠PBD,
即∠APB、∠PAC、∠PBD之间的关系不发生变化;
(2)如图②,

当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.
理由如下:∵l1∥l2,
∴∠PEC=∠PBD,
∵∠PEC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB.
当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.
如图③,

理由如下:∵l1∥l2,
∴∠PED=∠PAC,
∵∠PED=∠PBD+∠APB,
∴∠PAC=∠PBD+∠APB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,ABCD为长方形,其中点A、C坐标分别为(﹣8,4)、(2,﹣8),且AD∥x轴,交y轴于M点,AB交x轴于N.
(1)求B、D两点坐标和长方形ABCD的面积;
(2)一动点P从A出发(不与A点重合),以
 个单位/秒的速度沿AB向B点运动,在P点运动过程中,连接MP、OP,请直接写出∠AMP、∠MPO、∠PON之间的数量关系;
个单位/秒的速度沿AB向B点运动,在P点运动过程中,连接MP、OP,请直接写出∠AMP、∠MPO、∠PON之间的数量关系;(3)是否存在某一时刻t,使三角形AMP的面积等于长方形面积的
 ?若存在,求t的值并求此时点P的坐标;若不存在请说明理由.
?若存在,求t的值并求此时点P的坐标;若不存在请说明理由.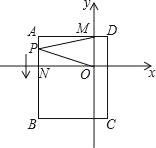
-
科目: 来源: 题型:
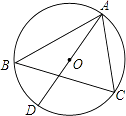
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AD是⊙O直径,若∠ABC=50°,则∠CAD=度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简或求值
(1)若A=-2a2+ab-b3,B=a2-2ab+b3,求A -2B的值。
(2)先化简,再求值:5x2y-3xy2-7(x2y- xy
 ),其中x=2,y=-1。
),其中x=2,y=-1。 -
科目: 来源: 题型:
查看答案和解析>>【题目】在东西向的马路上有一个巡岗亭A,巡岗员甲从岗亭A出发以13km/h速度匀速来回巡逻,如果规定向东巡逻为正,向西巡逻为负,巡逻情况记录如下:(单位:千米)
第一次
第二次
第三次
第四次
第五次
第六次
第七次
4
-5
3
-4
-3
6
-1
(1)求第六次结束时甲的位置(在岗亭A的东边还是西边?距离多远?)
(2)在第几次结束时距岗亭A最远?距离A多远?
(3)巡逻过程中配置无线对讲机,并一直与留守在岗亭A的乙进行通话,问在甲巡逻过程中,甲与乙的保持通话时长共多少小时?
-
科目: 来源: 题型:
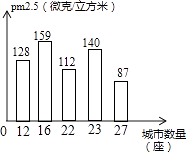
查看答案和解析>>【题目】如图是我校某班同学随机抽取的我国100座城市2017年某天当地pm2.5值的情况的条形统计图,那么本次调查中,PM2.5值的中位数为微克/立方米.
-
科目: 来源: 题型:
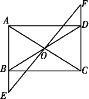
查看答案和解析>>【题目】如图所示,在矩形ABCD中,O是AC与BD的交点,过点O的直线EF与AB,CD的延长线分别交于点E,F.
(1)求证:△BOE≌△DOF;
(2)当EF与AC满足什么条件时,四边形AECF是菱形?并证明你的结论.
相关试题

