【题目】如图,∠AOB=30°,OC为∠AOB内部一条射线,点P为射线OC上一点,OP=4,点M、N分别为OA、OB边上动点,则△MNP周长的最小值为( )

A. 2 B. 4 C. ![]() D.
D. ![]()
参考答案:
【答案】B
【解析】
作点P关于OA的对称点P1,点P关于OB的对称点P2,连结P1P2,与OA的交点即为点M,与OB的交点即为点N,则此时M、N符合题意,求出线段P1P2的长即可.
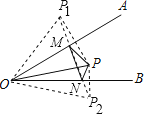
解:作点P关于OA的对称点P1,点P关于OB的对称点P2,连结P1P2,
与OA的交点即为点M,与OB的交点即为点N,此时△PMN的最小周长
∵点P关于OA的对称点为P1,关于OB的对称点为P2,连结OP1、OP2,
∴PM= P1M,OP=O P1,∠P1OA=∠POA;
∵点P关于OB的对称点为P2,
∴PN= P2N,OP=O P2,∠P2OB=∠POB,
∴OP1=OP2=OP=4,
∠P1OP2=∠P1OA+∠POA+∠POB+∠P2OB=2∠POA+2∠POB=2∠AOB=60°,
∴△OP1P2是等边三角形,
∴P1P2=OP1=4,
∴△PMN的最小周长为PM+MN+PN=P1M+MN+P2N=P1P2=4
即△PMN的周长的最小值是4.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,其对称轴为直线x=﹣1,给出下列结果:(1)b2>4ac;(2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)a﹣b+c<0.
则正确的结论是( )
A.(1)(2)(3)(4)
B.(2)(4)(5)
C.(2)(3)(4)
D.(1)(4)(5) -
科目: 来源: 题型:
查看答案和解析>>【题目】为了创建国家卫生城市,需要购买甲、乙两种类型的分类垃圾桶替换原来的垃圾桶,
 ,
, ,
, 三个小区所购买的数量和总价如表所示.
三个小区所购买的数量和总价如表所示.甲型垃圾桶数量(套)
乙型垃圾桶数量(套)
总价(元)











(1)问甲型垃圾桶、乙型垃圾桶的单价分别是每套多少元?
(2)求
 ,
, 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ABC=45
 ,AD,BE分别为BC、AC边上的高,AD、BE相交于点F,下列结论:
,AD,BE分别为BC、AC边上的高,AD、BE相交于点F,下列结论:①∠FCD=45

②AE=EC
③S△ABF:S△AFC=AD:FD
④若BF=2EC,则△FDC周长等于AB的长.
正确结论的序号是___________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC和△A1B1C1关于x轴成轴对称,画出△A1B1C1
(2)点C1的坐标为_________,△ABC的面积为__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有一系列等式:
1×2×3×4+1=52=(12+3×1+1)2,
2×3×4×5+1=112=(22+3×2+1)2,
3×4×5×6+1=192=(32+3×3+1)2,
4×5×6×7+1=292=(42+3×4+1)2,
……
(1)根据你的观察,归纳发现规律,写出9×10×11×12+1的结果是________ ;
(2)式子(n-1) n (n+1) (n+2)+1=___________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列推理过程,在括号中填写理由. 已知:如图,点D,E分别在线段AB、BC上,AC∥DE,DF∥AE交BC于点F,AE平分∠BAC.求证:DF平分∠BDE
证明:∵AE平分∠BAC(已知)
∴∠1=∠2(________)
∵AC∥DE(已知)
∴∠1=∠3(________)
故∠2=∠3(________)
∵DF∥AE(已知)
∴∠2=∠5(________)
∴∠3=∠4(________)
∴DE平分∠BDE(________)

相关试题

