搜索
【题目】（1）先化简，再求值 x（x﹣1）+2x（x+1）﹣（3x﹣1）（2x﹣5），其中 x=2．
（2）解方程（3x﹣2）（2x﹣3）=（6x+5）（x﹣1）+15．
参考答案：
【答案】（1）﹣3x2+18x﹣5，19；（2）x=﹣ 
．
【解析】
（1）根据整式的混合运算法则把原式化简，代入计算即可；
（2）根据整式的混合运算法则把原方程变形，根据一元一次方程的解法解出方程．
（1）原式=x2-x+2x2+2x-（6x2-17x+5）
=x2-x+2x2+2x-6x2+17x-5
=-3x2+18x-5
当x=2时，原式=-3×22+18×2-5=19；
（2）（3x-2）（2x-3）=（6x+5）（x-1）+15
6x2-13x+6=6x2-x+10
-12x=4，
x=-．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图：直线 a，b，c 表示三条相互交叉而建的公路，现在要建立一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（ ）
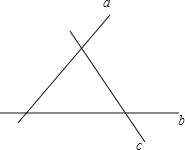
A. 1 个 B. 2 个 C. 3 个 D. 4 个
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，小敏在测量学校一幢教学楼AB的高度时，她先在点C测得教学楼的顶部A的仰角为30°，然后向教学楼前进12米到达点D，又测得点A的仰角为45°．请你根据这些数据，求出这幢教学楼AB的高度．
（结果精确到0.1米，参考数据：
≈1.73）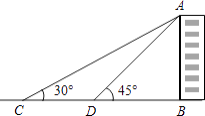
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，E是CD上一点，DF⊥BE交BE的延长线于点G，交BC的延长线于点F．
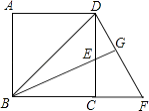
（1）求证：△BCE≌△DCF．
（2）若∠DBE=∠CBE，求证：BD=BF．
（3）在（2）的条件下，求CE：ED的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】．如图①，在△ABC 中，D、E 分别是 AB、AC 上的点，AB=AC，AD=AE，然后将△ADE 绕点 A 顺时针旋转一定角度，连接 BD，CE，得到图②，将 BD、CE 分别延长至 M、N，使 DM=
BD，EN=CE，得到图③，请解答下列问题：（1）在图②中，BD 与 CE 的数量关系是 ；
（2）在图③中，猜想 AM 与 AN 的数量关系，∠MAN 与∠BAC 的数量关系，并证明你的猜想．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知直线y=﹣x+3与x轴、y轴分别交于A，B两点，抛物线y=﹣x2+bx+c经过A，B两点，点P在线段OA上，从点A以1个单位/秒的速度匀速运动；同时，点Q在线段AB上，从点A出发，向点B以
个单位/秒的速度匀速运动，连接PQ，设运动时间为t秒．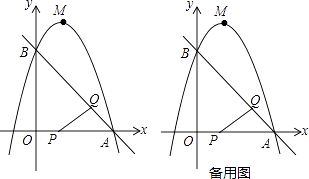
（1）求抛物线的解析式；
（2）当t为何值时，△APQ为直角三角形；
（3）过点P作PE∥y轴，交AB于点E，过点Q作QF∥y轴，交抛物线于点F，连接EF，当EF∥PQ时，求点F的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】分别写有数0，2﹣1 ， ﹣2，cos30°，3的五张卡片，除数字不同外其他均相同，从中任意抽取一张，那么抽到非负数的概率是（ ）
A.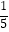
B.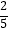
C.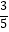
D.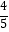
相关试题
