【题目】某班同学组织春游活动,到超市选购A, B两种饮料,若购买6瓶A种饮料, 4瓶B种饮料需花费39元,购买20瓶A种饮料和30瓶B种饮料需花费180元。
(1)购买A, B两种饮料每瓶各多少元?
(2)实际购买时,恰好超市进行促销活动,如果一次性购买 A种饮料数量超过20瓶,则超出部分的价格享受八折优惠,B种饮料价格保持不变,若购买B种饮料的数量是A种饮料数量的2倍还多10瓶,且总费用不超过320元则最多可购买A种饮料多少瓶?
参考答案:
【答案】(1)A、B两种饮料每瓶各为4.5元、3元;(2)最多购买A种饮料28瓶
【解析】
(1)分别利用购买6瓶A种饮料和4瓶B种饮料需花费39元,购买20瓶A种饮料和30瓶B种饮料需花费180元分别得出等式求出即可;
(2)分别表示出购买两种饮料的费用,进而得出不等式求出答案.
解:(1)设A、B两种饮料每瓶各为x,y元
![]() ,解得x=4.5,y=3.
,解得x=4.5,y=3.
答:购进A种饮料每瓶4.5元,购进B种饮料每瓶3元;
(2)设购进A种饮料a瓶,购进B种饮料(2a+10)瓶,根据题意可得;
20×4.5+4.5(a20)×80%+3(2a+10)320,
解得:a28![]() ,
,
∵a取正整数,
∴a最大为28,
答:最多可购进A种饮料28瓶
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:正方形ABCD,E是BC的中点,连接AE,过点B作射线BM交正方形的一边于点F,交AE于点O.
(1)若BF⊥AE,
①求证:BF=AE;
②连接OD,确定OD与AB的数量关系,并证明;
(2)若正方形的边长为4,且BF=AE,求BO的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在8×8的网格中的每个小正方形边长都是1,线段交点称作格点.任意连接这些格点,可得到一些线段.按要求作图:
(1)请画出△ABC的高AD;
(2)请连接格点,用一条线段将图中△ABC分成面积相等的两部分;
(3)直接写出△ABC的面积是_____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠CBF为( )
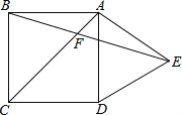
A.75°B.60°C.55°D.45°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在三角形ABC中,点D在BC上,DE⊥AB于E,点F在AB上,在CF的延长线上取一点G,连接AG.
(1)如图1,若∠GAB=∠B,∠GAC+∠EDB=180°,求证:AB⊥AC.
(2)如图2.在(1)的条件下,∠GAC的平分线交CG于点M,∠ACB的平分线交AB于点N,当∠AMC∠ANC=35°时,求∠AGC的度数。
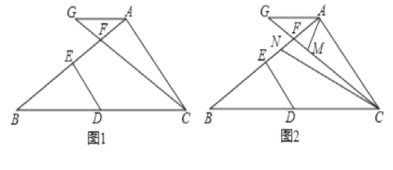
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=10,BC=4,Q为AB边的中点,P为CD边上的动点,且△AQP是腰长为5的等腰三角形,则CP的长为_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(8,6),C(0,10),AC=CO,直线AC交x轴于点M,将△AOC沿直线AC翻折,使得点O落在点B处,连接AB交x轴于D,动点P从点O出发,以2个单位长度/秒的速度沿射线OA运动;同时动点Q从A出发以每秒1个单位的速度沿射线AB运动。

(1)求B点的坐标;
(2)连接PB,设点P的运动时间为t秒,△PAB的面积为S,求S与t的关系式,并直接写t的取值范围;
(3)在点P、Q运动过程中,当t为何值时,△APQ是以PQ为底边的等腰三角形?并直接写出Q点坐标。
相关试题

