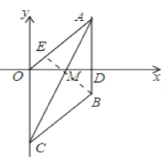
【题目】如图,在平面直角坐标系中,A(8,6),C(0,10),AC=CO,直线AC交x轴于点M,将△AOC沿直线AC翻折,使得点O落在点B处,连接AB交x轴于D,动点P从点O出发,以2个单位长度/秒的速度沿射线OA运动;同时动点Q从A出发以每秒1个单位的速度沿射线AB运动。

(1)求B点的坐标;
(2)连接PB,设点P的运动时间为t秒,△PAB的面积为S,求S与t的关系式,并直接写t的取值范围;
(3)在点P、Q运动过程中,当t为何值时,△APQ是以PQ为底边的等腰三角形?并直接写出Q点坐标。
参考答案:
【答案】(1)(8,-4);(2)s=16t+80,0t5;(3)t=![]() ,(8,
,(8, ![]() )
)
.
【解析】
(1)根据翻折的性质,可得OA=AB,OC=BC,根据菱形的判定与性质,可得![]() ;
;
(2)根据勾股定理,可得OB,AC的长,根据菱形的面积,可得BE的长,根据三角形的面积公式,可得函数关系式;
根据OP与OA的关系,可得自变量的取值范围;
(3)根据线段的和差,可得AP,根据等腰三角形的定义,可得关于t的方程,根据解方程,可得答案.
(1)由△AOC沿直线AC翻折,使得点O落在点B处,得
OA=AB,OC=BC.
由AC=CO=10,得
AO=CO=CB=BA=10.
四边形AOCB是菱形,
![]() ,即x
,即x![]() =8,
=8,
![]() ,即y
,即y![]() =610=4,
=610=4,
即B点坐标(8,4);
(2)如图作BE⊥OA于E,
由勾股定理,得
OB=![]() ,AC=
,AC=![]() =8
=8![]() ,
,
由菱形的面积,得
OABE=ACOB,
即BE=4![]() ×8
×8![]() ÷10=16,
÷10=16,
OP=2t,AP=102t,
S△ABP=![]() APBE=
APBE=![]() (102t)×16=16t+80,
(102t)×16=16t+80,
S与t的关系式为s=16t+80,
由OPAO,即2t10,解得t5,
由时间是非负数,得t0,
自变量的取值范围是0t5;
(3)由OP=2t,得AP=OAOP=102t.
AQ=t.
由AP=AQ,得
102t=t.
解得t=![]() ,
,
当t=![]() 时,△APQ是以PQ为底边的等腰三角形;
时,△APQ是以PQ为底边的等腰三角形;
由AB∥y轴,得
Q点的横坐标为8,纵坐标为6![]() =
=![]() ,
,
即Q点的坐标为(8, ![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班同学组织春游活动,到超市选购A, B两种饮料,若购买6瓶A种饮料, 4瓶B种饮料需花费39元,购买20瓶A种饮料和30瓶B种饮料需花费180元。
(1)购买A, B两种饮料每瓶各多少元?
(2)实际购买时,恰好超市进行促销活动,如果一次性购买 A种饮料数量超过20瓶,则超出部分的价格享受八折优惠,B种饮料价格保持不变,若购买B种饮料的数量是A种饮料数量的2倍还多10瓶,且总费用不超过320元则最多可购买A种饮料多少瓶?
-
科目: 来源: 题型:
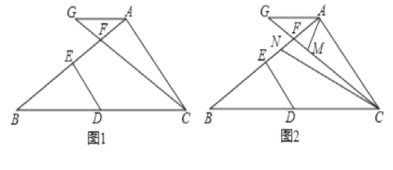
查看答案和解析>>【题目】已知,在三角形ABC中,点D在BC上,DE⊥AB于E,点F在AB上,在CF的延长线上取一点G,连接AG.
(1)如图1,若∠GAB=∠B,∠GAC+∠EDB=180°,求证:AB⊥AC.
(2)如图2.在(1)的条件下,∠GAC的平分线交CG于点M,∠ACB的平分线交AB于点N,当∠AMC∠ANC=35°时,求∠AGC的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=10,BC=4,Q为AB边的中点,P为CD边上的动点,且△AQP是腰长为5的等腰三角形,则CP的长为_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2;
②方程
 的两个根是x1=﹣1,x2=3;
的两个根是x1=﹣1,x2=3;③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
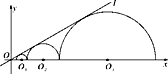
查看答案和解析>>【题目】如图,圆心都在x轴正半轴上的半圆O1,半圆O2,…,半圆On与直线l相切.设半圆O1,半圆O2,…,半圆On的半径分别是r1,r2,…,rn,则当直线l与x轴所成锐角为30°,且r1=1时,r2018=_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某摩托车厂本周计划每日生产450辆摩托车,由于工人实行轮休, 每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表: [增加的辆数为正数,减少的辆数为负数]
星期
一
二
三
四
五
六
日
增减
-5
+7
-3
+4
+10
-9
-25
(1)本周星期六生产多少辆摩托车?
(2)本周总产量与计划产量相比,是增加了还是减少了?为什么?
(3)产量最多的那天比产量最少的那天多生产多少辆?
相关试题

