【题目】如图,在直角坐标平面上,△AOB是直角三角形,点O在原点上,A、B两点的坐标分别为(-1,y1)、(3,y2),线段AB交y轴于点C.若S△AOC=1,记∠AOC为α,∠BOC为β,则sin α·sin β的值为____.

参考答案:
【答案】![]()
【解析】分析:首先过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,由A、B两点的坐标分别为(-1,y1)、(3,y2),S△AOC=1,可求得OD,OE,OC的长,继而求得△AOB的面积,求得OAOB的值,又由三角函数的定义,即可求得答案.
详解:过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,
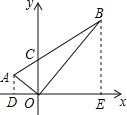
∵A、B两点的坐标分别为(-1,y1)、(3,y2),
∴OD=1,OE=3,
∵S△AOC=1,
∴![]() OCOD=1,
OCOD=1,
∴OC=2,
∴SRt△AOB=S△AOC+S△BOC=1+![]() OCOE=1+3=4,
OCOE=1+3=4,
∴![]() OAOB=4,
OAOB=4,
∴OAOB=8,
∵OA∥OC∥BE,
∴∠OAD=∠AOC=α,∠OBE=∠BOC=β,
∴sinαsinβ=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
 与一次函数y=k2x-k2+2在同一直角坐标系中的图象相交于A,B两点,其中A(-1,3),直线y=k2x-k2+2与坐标轴分别交于C,D两点,下列说法:①k1,k2<0;②点B的坐标为(3,-1);③当x<-1时,
与一次函数y=k2x-k2+2在同一直角坐标系中的图象相交于A,B两点,其中A(-1,3),直线y=k2x-k2+2与坐标轴分别交于C,D两点,下列说法:①k1,k2<0;②点B的坐标为(3,-1);③当x<-1时, <k2x-k2+2;④tan∠OCD=-
<k2x-k2+2;④tan∠OCD=-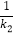 ,其中正确的是( )
,其中正确的是( )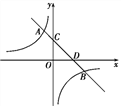
A. ①③ B. ①②④ C. ①③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,已知∠1=∠2,∠C=∠D

(1)判断BD与CE是否平行,并说明理由;(2)说明∠A=∠F的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=x-2与y轴交于点C,与x轴交于点B,与反比例函数y=
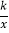 的图象在第一象限交于点A,连接OA,若S△AOB∶S△BOC=1∶2,则k的值为____.
的图象在第一象限交于点A,连接OA,若S△AOB∶S△BOC=1∶2,则k的值为____.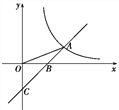
-
科目: 来源: 题型:
查看答案和解析>>【题目】知识链接:
“转化、化归思想”是数学学习中常用的一种探究新知、解决问题的基本的数学思想方法,通过“转化、化归”通常可以实现化未知为已知,化复杂为简单,从而使问题得以解决.
(1)问题背景:已知:△ABC.试说明:∠A+∠B+∠C=180°.
问题解决:(填出依据)
解:(1)如图①,延长AB到E,过点B作BF∥AC.
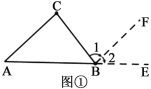
∵BF∥AC(作图)
∴∠1=∠C( )
∠2=∠A( )
∵∠2+∠ABC+∠1=180°(平角的定义)
∴∠A+∠ABC+∠C=180°(等量代换)
小结反思:本题通过添加适当的辅助线,把三角形的三个角之和转化成了一个平角,利用平角的定义,说明了数学上的一个重要结论“三角形的三个内角和等于180°.”
(2)类比探究:请同学们参考图②,模仿(1)的解决过程试说明“三角形的三个内角和等于180°”
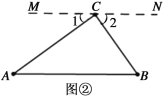
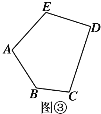
(3)拓展探究:如图③,是一个五边形,请直接写出五边形ABCDE的五个内角之和∠A+∠B+∠C+∠D+∠E= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数
 (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在综合与实践课上,老师请同学们以“两条平行线
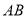 ,
,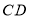 和一块含
和一块含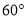 角的直角三角尺
角的直角三角尺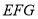 (
(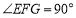 ,
,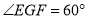 )”为主题开展数学活动.
)”为主题开展数学活动.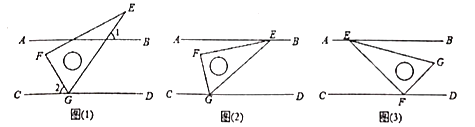
(1)如图(1),把三角尺的
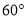 角的顶点
角的顶点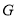 放在
放在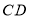 上,若
上,若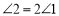 ,求
,求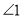 的度数;
的度数;(2)如图(2),小颖把三角尺的两个锐角的顶点
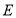 、
、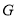 分别放在
分别放在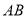 和
和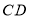 上,请你探索并说明
上,请你探索并说明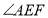 与
与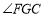 之间的数量关系;
之间的数量关系;(3)如图(3),小亮把三角尺的直角顶点
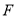 放在
放在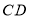 上,
上,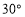 角的顶点
角的顶点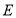 落在
落在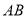 上.若
上.若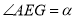 ,
,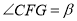 ,请用含
,请用含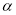 ,
,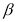 的式子直接表示
的式子直接表示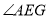 与
与 的数量关系.
的数量关系.
相关试题

