【题目】在综合与实践课上,老师请同学们以“两条平行线![]() ,
,![]() 和一块含
和一块含![]() 角的直角三角尺
角的直角三角尺![]() (
(![]() ,
,![]() )”为主题开展数学活动.
)”为主题开展数学活动.
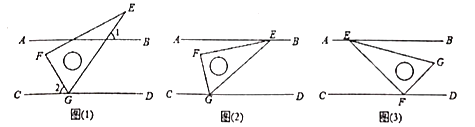
(1)如图(1),把三角尺的![]() 角的顶点
角的顶点![]() 放在
放在![]() 上,若
上,若![]() ,求
,求![]() 的度数;
的度数;
(2)如图(2),小颖把三角尺的两个锐角的顶点![]() 、
、![]() 分别放在
分别放在![]() 和
和![]() 上,请你探索并说明
上,请你探索并说明![]() 与
与![]() 之间的数量关系;
之间的数量关系;
(3)如图(3),小亮把三角尺的直角顶点![]() 放在
放在![]() 上,
上,![]() 角的顶点
角的顶点![]() 落在
落在![]() 上.若
上.若![]() ,
,![]() ,请用含
,请用含![]() ,
,![]() 的式子直接表示
的式子直接表示![]() 与
与![]() 的数量关系.
的数量关系.
参考答案:
【答案】(1)∠1=40°;(2)∠AEF+∠FGC=90°;(3)α+β=300°.
【解析】
(1)通过![]() ,得出
,得出![]() ,再通过
,再通过![]() 求出∠1的度数;
求出∠1的度数;
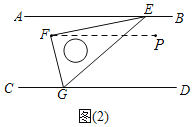
(2)如图,过点F作![]() ,通过
,通过![]() ,解得
,解得![]() ,从而求出
,从而求出![]() 的度数;
的度数;
(3)根据![]() 得出
得出![]() ,代入求出
,代入求出![]() 的度数.
的度数.
解:(1)∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,解得
,解得![]() ;
;
(2)如图,过点F作![]() ,
,
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]()
∵![]() ,
,
∴![]() ;
;
(3)![]() .
.
∵![]()
∴![]()
即![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标平面上,△AOB是直角三角形,点O在原点上,A、B两点的坐标分别为(-1,y1)、(3,y2),线段AB交y轴于点C.若S△AOC=1,记∠AOC为α,∠BOC为β,则sin α·sin β的值为____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】知识链接:
“转化、化归思想”是数学学习中常用的一种探究新知、解决问题的基本的数学思想方法,通过“转化、化归”通常可以实现化未知为已知,化复杂为简单,从而使问题得以解决.
(1)问题背景:已知:△ABC.试说明:∠A+∠B+∠C=180°.
问题解决:(填出依据)
解:(1)如图①,延长AB到E,过点B作BF∥AC.
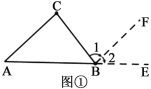
∵BF∥AC(作图)
∴∠1=∠C( )
∠2=∠A( )
∵∠2+∠ABC+∠1=180°(平角的定义)
∴∠A+∠ABC+∠C=180°(等量代换)
小结反思:本题通过添加适当的辅助线,把三角形的三个角之和转化成了一个平角,利用平角的定义,说明了数学上的一个重要结论“三角形的三个内角和等于180°.”
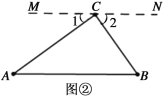
(2)类比探究:请同学们参考图②,模仿(1)的解决过程试说明“三角形的三个内角和等于180°”
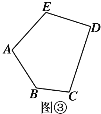
(3)拓展探究:如图③,是一个五边形,请直接写出五边形ABCDE的五个内角之和∠A+∠B+∠C+∠D+∠E= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数
 (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位计划在暑假阴间组织员工到某地旅游,参加旅游的人数估计为10~25人,甲、乙两家旅行社的服务质量相同,且报价都是每人200元.经过协商,甲旅行社表示可给予每位游客七折优惠;乙旅行社表示可先免去一位游客的费用,其余游客七五折优惠.设该单位参加旅游的人数是x人.选择甲旅行社时,所需费用为
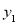 元,选择乙旅行社时,所需费用为
元,选择乙旅行社时,所需费用为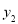 元.
元.(1)写出甲旅行社收费
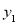 (元)与参加旅游的人数x(人)之间的关系式.
(元)与参加旅游的人数x(人)之间的关系式.(2)写出乙旅行社收费
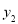 (元)与参加旅游的人数x(人)之间的关系式.
(元)与参加旅游的人数x(人)之间的关系式.(3)该单位选择哪一家旅行社支付的旅游费用较少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一列式子,按一定规律排列成
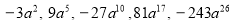 , ….
, ….(1)当a =1时,其中三个相邻数的和是63,则位于这三个数中间的数是________;
(2)上列式子中第n个式子为_____________(n为正整数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直线AB与x轴、y轴相交于
 、
、 两点,动点C在线段OA上(不与O、A重合),将线段CB绕着点C顺时针旋转
两点,动点C在线段OA上(不与O、A重合),将线段CB绕着点C顺时针旋转 得到CD,当点D恰好落在直线AB上时,过点D作
得到CD,当点D恰好落在直线AB上时,过点D作 轴于点E.
轴于点E.
(1)求证,
 ;
;(2)如图2,将
 沿x轴正方向平移得
沿x轴正方向平移得 ,当直线
,当直线 经过点D时,求点D的坐标及
经过点D时,求点D的坐标及 平移的距离;
平移的距离;
(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐标,若不存在,请说明理由.
相关试题

