【题目】(7分)如图,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]()
![]() 在第一象限
在第一象限
的图象交于![]() 点,过
点,过![]() 点作
点作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,已知
,已知![]() 的面积为1.
的面积为1.
(1)求反比例函数的解析式;
(2)如果![]() 为反比例函数在第一象限图象上的点(点
为反比例函数在第一象限图象上的点(点![]() 与点
与点![]() 不重合),且
不重合),且![]() 点的横坐标为1,在
点的横坐标为1,在![]() 轴上求一点
轴上求一点![]() ,使
,使![]() 最小.
最小.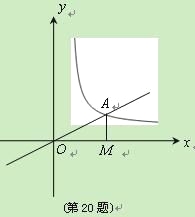
参考答案:
【答案】解:(1)设![]() 点的坐标为(
点的坐标为(![]() ,
,![]() ),则
),则![]() .∴
.∴![]() .
.
∵![]() ,∴
,∴![]() .∴
.∴![]() .
.
∴反比例函数的解析式为![]() .··································································· 3分
.··································································· 3分
(2) 由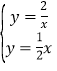 得
得![]() ∴
∴![]() 为(
为(![]() ,
,![]() ). ·············································· 4分
). ·············································· 4分
设![]() 点关于
点关于![]() 轴的对称点为
轴的对称点为![]() ,则
,则![]() 点的坐标为(
点的坐标为(![]() ,
,![]() ).
).
令直线![]() 的解析式为
的解析式为![]() .
.
∵![]() 为(
为(![]() ,
,![]() )∴
)∴![]() ∴
∴![]()
∴![]() 的解析式为
的解析式为![]() .···································································· 6分
.···································································· 6分
当![]() 时,
时,![]() .∴
.∴![]() 点为(
点为(![]() ,
,![]() ). ······················································ 7分
). ······················································ 7分
【解析】
试题(1)设出A点的坐标,然后根据△OAM的面积为1,确定出k的值即可;(2)分别求出点A、B的坐标以及点A关于![]() 轴的对称点C的坐标,然后求出直线BC的解析式,直线BC与x轴的交点即为所求.
轴的对称点C的坐标,然后求出直线BC的解析式,直线BC与x轴的交点即为所求.
试题解析:(1)设A点的坐标为(![]() ,
,![]() ),
),
则![]() .∴
.∴![]() .
.
∵![]() ,∴
,∴![]() .∴
.∴![]() .
.
∴反比例函数的解析式为![]() .
.
(2) 由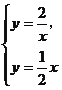 得
得![]() 或
或![]() ∴A为
∴A为![]() .
.
设A点关于![]() 轴的对称点为C,则C点的坐标为
轴的对称点为C,则C点的坐标为![]() .
.
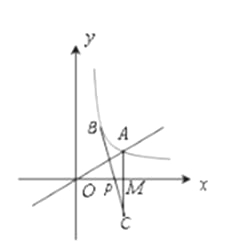
如要在![]() 轴上求一点P,使PA+PB最小.则P点应为BC和x轴的交点,如图所示.
轴上求一点P,使PA+PB最小.则P点应为BC和x轴的交点,如图所示.
令直线BC的解析式为![]() .
.
∵B为(![]() ,
,![]() ),∴
),∴![]() ∴
∴![]()
∴BC的解析式为![]() .
.
当![]() 时,
时,![]() .∴P点坐标为
.∴P点坐标为 .
.
-
科目: 来源: 题型:
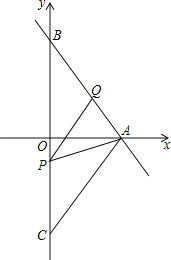
查看答案和解析>>【题目】如图,己知函数y=﹣
 x+4的图象与坐标轴的交点分别为点A、B,点C与点B关于x轴对称,动点P、Q分别在线段BC、AB上(点P不与点B、C重合).且∠APQ=∠ABO
x+4的图象与坐标轴的交点分别为点A、B,点C与点B关于x轴对称,动点P、Q分别在线段BC、AB上(点P不与点B、C重合).且∠APQ=∠ABO(1)点A的坐标为 ,AC的长为 ;
(2)判断∠BPQ与∠CAP的大小关系,并说明理由;
(3)当△APQ为等腰三角形时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列选项中,是反比例函数关系的为
A. 在直角三角形中,30°角所对的直角边y与斜边x之间的关系
B. 在等腰三角形中,顶角y与底角x之间的关系
C. 圆的面积S与它的直径d之间的关系
D. 面积为20的菱形,其中一条对角线y与另一条对角线x之间的关系
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A、B两点,若反比例函数
 (x>0)的图像与△ABC有公共点,则k的取值范围是( )
(x>0)的图像与△ABC有公共点,则k的取值范围是( )
A. 2≤k≤9 B. 2≤k≤8 C. 2≤k≤5 D. 5≤k≤8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1和∠2互为补角,∠A=∠D.求证:AB∥CD.
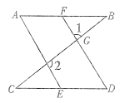
证明:∵∠1与∠CGD是对顶角,
∴∠1=∠CGD(______).
又∠1和∠2互为补角(已知),
∴∠CGD和∠2互为补角,
∴AE∥FD(_________),
∴∠A=∠BFD(_______).
∵∠A=∠D(已知),
∴∠BFD=∠D(_______),
AB∥CD(______).
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)计算:(tan60°)﹣1×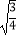 ﹣|﹣
﹣|﹣  |+23×0.125
|+23×0.125
(2)解方程:(x﹣5)2=16. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是某一蓄水池的排水速度
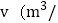 h)与排完水池中的水所用的时间t(h)之间的函数关系图象.
h)与排完水池中的水所用的时间t(h)之间的函数关系图象. 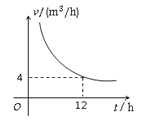
(1)请你根据图象提供的信息求出此蓄水池的蓄水量;
(2)写出此函数的解析式;
(3)若要6 h排完水池中的水,那么每小时的排水量应该是多少?
(4)如果每小时排水量是
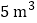 ,那么水池中的水要用多少小时排完?
,那么水池中的水要用多少小时排完?
相关试题

