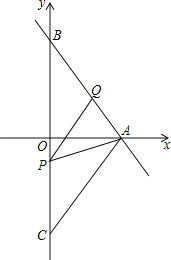
【题目】如图,己知函数y=﹣![]() x+4的图象与坐标轴的交点分别为点A、B,点C与点B关于x轴对称,动点P、Q分别在线段BC、AB上(点P不与点B、C重合).且∠APQ=∠ABO
x+4的图象与坐标轴的交点分别为点A、B,点C与点B关于x轴对称,动点P、Q分别在线段BC、AB上(点P不与点B、C重合).且∠APQ=∠ABO
(1)点A的坐标为 ,AC的长为 ;
(2)判断∠BPQ与∠CAP的大小关系,并说明理由;
(3)当△APQ为等腰三角形时,求点P的坐标.
参考答案:
【答案】(1)(3,0),5;(2)见解析;(3)P点坐标为(0,﹣1),(0,![]() ).
).
【解析】
试题分析:(1)利用坐标轴上点的坐标特征可求出A、B点的坐标,再利用关于x轴对称的点的坐标特征得到C点坐标,然后利用勾股定理可计算出AC的长;
(2)利用对称性质得到AB=AC,则∠1=∠2,而∠APQ=∠1,所以∠2=∠APQ,再根据三角形外角性质得∠BPA=∠2+∠3,易得∠BPQ=∠3;
(3)分类讨论:当PA=PQ,如图1,根据等腰三角形的性质得∠PQA=∠PAQ,利用三角形外角性质和等量代换可得∠PQA=∠BPA,则BP=BA=5,所以OP=BP﹣OB=1,于是得到此时P点坐标为(0,﹣1);当AQ=AP,由于∠AQP=∠APQ,∠AQP=∠BPA,两者相矛盾,此情况不存在;当QA=QP,如图2,则∠APQ=∠PAQ,由于∠1=∠APQ,则∠1=∠PAQ,所以PA=PB,设P(0,t),则PB=PA=4﹣t,在Rt△OPA中利用勾股定理得到t2+32=(4﹣t)2,解得t=![]() ,从而可得到此时P点坐标为(0,
,从而可得到此时P点坐标为(0,![]() ).
).
解:(1)当y=0时,﹣![]() x+4=0,解得x=3,则A(3,0),
x+4=0,解得x=3,则A(3,0),
当x=0时,y=﹣![]() x+4=4,则B(0,4),
x+4=4,则B(0,4),
∵点C与点B关于x轴对称,
∴C(0,﹣4),
∴AC=![]() =5;
=5;
故答案为(3,0),5;
(2)∠BPQ=∠CAP.理由如下:
∵点C与点B关于x轴对称,
∴AB=AC,
∴∠1=∠2,
∵∠APQ=∠1,
∴∠2=∠APQ,
∵∠BPA=∠2+∠3,
即∠BPQ+∠APQ=∠2+∠3,
∴∠BPQ=∠3;
(3)当PA=PQ,如图1,则∠PQA=∠PAQ,
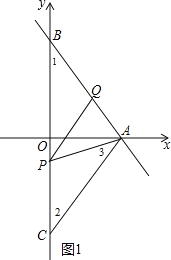
∵∠PQA=∠1+∠BPQ=∠APQ+∠BPQ=∠BPA,
∴BP=BA=5,
∴OP=BP﹣OB=1,
∴P(0,﹣1);
当AQ=AP,则∠AQP=∠APQ,
而∠AQP=∠BPA,所以此情况不存在;
当QA=QP,如图2,则∠APQ=∠PAQ,
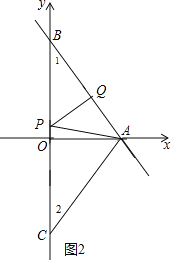
而∠1=∠APQ,
∴∠1=∠PAQ,
∴PA=PB,
设P(0,t),则PB=4﹣t,
∴PA=4﹣t,
在Rt△OPA中,∵OP2+OA2=PA2,
∴t2+32=(4﹣t)2,解得t=![]() ,
,
∴P(0,![]() ),
),
综上所述,满足条件的P点坐标为(0,﹣1),(0,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在
 处,
处, 交AD于点E.
交AD于点E.(1)试判断△BDE的形状,并说明理由;
(2)若
 ,
, ,求△BDE的面积.
,求△BDE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB、BC、AC三边的长分别为
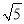 ,
, 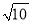 ,
, 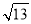 ,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.(1)△ABC的面积为 .
(2)若△DEF的三边DE、EF、DF长分别为
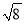 ,
, 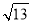 ,
, 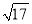 ,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .(3)在△ABC中,AB=2
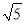 ,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .
,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .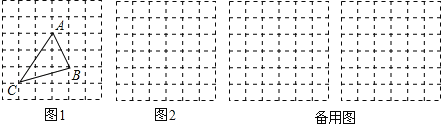
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
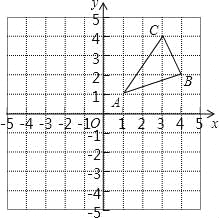
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;
(3)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列选项中,是反比例函数关系的为
A. 在直角三角形中,30°角所对的直角边y与斜边x之间的关系
B. 在等腰三角形中,顶角y与底角x之间的关系
C. 圆的面积S与它的直径d之间的关系
D. 面积为20的菱形,其中一条对角线y与另一条对角线x之间的关系
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A、B两点,若反比例函数
 (x>0)的图像与△ABC有公共点,则k的取值范围是( )
(x>0)的图像与△ABC有公共点,则k的取值范围是( )
A. 2≤k≤9 B. 2≤k≤8 C. 2≤k≤5 D. 5≤k≤8
-
科目: 来源: 题型:
查看答案和解析>>【题目】(7分)如图,正比例函数
 的图象与反比例函数
的图象与反比例函数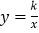
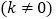 在第一象限
在第一象限的图象交于
 点,过
点,过 点作
点作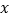 轴的垂线,垂足为
轴的垂线,垂足为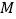 ,已知
,已知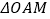 的面积为1.
的面积为1.(1)求反比例函数的解析式;
(2)如果
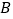 为反比例函数在第一象限图象上的点(点
为反比例函数在第一象限图象上的点(点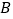 与点
与点 不重合),且
不重合),且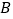 点的横坐标为1,在
点的横坐标为1,在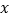 轴上求一点
轴上求一点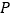 ,使
,使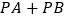 最小.
最小.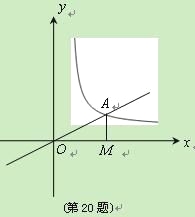
相关试题

