【题目】如图所示是某一蓄水池的排水速度![]() h)与排完水池中的水所用的时间t(h)之间的函数关系图象.
h)与排完水池中的水所用的时间t(h)之间的函数关系图象.
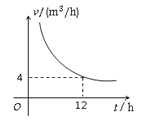
(1)请你根据图象提供的信息求出此蓄水池的蓄水量;
(2)写出此函数的解析式;
(3)若要6 h排完水池中的水,那么每小时的排水量应该是多少?
(4)如果每小时排水量是![]() ,那么水池中的水要用多少小时排完?
,那么水池中的水要用多少小时排完?
参考答案:
【答案】(1)48(![]() ) (2)
) (2)![]() (3)
(3)![]() . (4)9.6
. (4)9.6
【解析】分析: (1)观察图象易知蓄水池的蓄水量;
(2)![]() 与
与![]() 之间是反比例函数关系,所以可以设
之间是反比例函数关系,所以可以设![]() ,依据图象上点(12,4)的坐标可以求得
,依据图象上点(12,4)的坐标可以求得![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)求当![]() h时
h时![]() 的值.
的值.
(4)求当![]() h时,t的值.
h时,t的值.
解:(1)蓄水池的蓄水量为12×4=48(![]() ).
).
(2)函数的解析式为![]() .
.
(3)![]() .
.
(4)依题意有![]() ,解得
,解得![]() (h).
(h).
所以如果每小时排水量是5 ![]() ,那么水池中的水将要9.6小时排完.
,那么水池中的水将要9.6小时排完.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(7分)如图,正比例函数
 的图象与反比例函数
的图象与反比例函数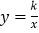
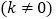 在第一象限
在第一象限的图象交于
 点,过
点,过 点作
点作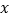 轴的垂线,垂足为
轴的垂线,垂足为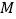 ,已知
,已知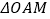 的面积为1.
的面积为1.(1)求反比例函数的解析式;
(2)如果
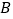 为反比例函数在第一象限图象上的点(点
为反比例函数在第一象限图象上的点(点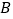 与点
与点 不重合),且
不重合),且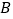 点的横坐标为1,在
点的横坐标为1,在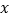 轴上求一点
轴上求一点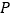 ,使
,使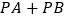 最小.
最小.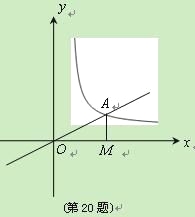
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1和∠2互为补角,∠A=∠D.求证:AB∥CD.
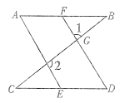
证明:∵∠1与∠CGD是对顶角,
∴∠1=∠CGD(______).
又∠1和∠2互为补角(已知),
∴∠CGD和∠2互为补角,
∴AE∥FD(_________),
∴∠A=∠BFD(_______).
∵∠A=∠D(已知),
∴∠BFD=∠D(_______),
AB∥CD(______).
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)计算:(tan60°)﹣1×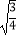 ﹣|﹣
﹣|﹣  |+23×0.125
|+23×0.125
(2)解方程:(x﹣5)2=16. -
科目: 来源: 题型:
查看答案和解析>>【题目】若反比例函数y=
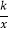 与一次函数y=2x-4的图象都经过点A(a,2).
与一次函数y=2x-4的图象都经过点A(a,2).(1)求反比例函数y=
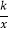 的表达式;
的表达式;(2)当反比例函数y=
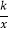 的值大于一次函数y=2x-4的值时,求自变量x的取值范围.
的值大于一次函数y=2x-4的值时,求自变量x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在两个不透明的口袋中分别装有三个颜色分别为红色、白色、绿色的小球,这三个小球除颜色外其他都相同,
(1)在其中一个口袋中一次性随机摸出两个球,请写出在这一过程中的一个必然事件;
(2)若分别从两个袋中随机取出一个球,试求出两个小球颜色相同的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB∥CD,∠1=∠2,∠3=∠4.
(1)求证:AD∥BE;
(2)若∠B=∠3=2∠2,求∠D的度数.

相关试题

