【题目】如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADB+∠EDC=120°. 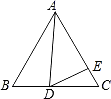
(1)求证:△ABD∽△DCE;
(2)若BD=3,CE=2,求△ABC的边长.
参考答案:
【答案】
(1)解:∵△ABC为正三角形,
∴∠B=∠C=60°,
∴∠ADB+∠BAD=120°,
∵∠ADB+∠CDE=120°,
∴∠BAD=∠CDE,
∴△ABD∽△DCE
(2)解:∵△ABD∽△DCE
∴ ![]() ,
,
设正三角形边长为x,
则 ![]() ,
,
解得x=9,
即△ABC的边长为9
【解析】(1)根据等边三角形性质求出∠B=∠C=60°,根据等式性质求出∠BAD=∠CDE,即可证明△ABD∽△DCE;(2)由(1)知道△ABD∽△DCE,对应边成比例得出 ![]() ,列方程解答即可.
,列方程解答即可.
【考点精析】认真审题,首先需要了解相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售甲、乙两种商品,现有如下信息: 请结合以上信息,解答下列问题:

(1)求甲、乙两种商品的进货单价;
(2)已知甲、乙两种商品的零售单价分别为2元、3元,该商店平均每天卖出甲商品500件和乙商品1300件,经市场调查发现,甲种商品零售单价每降0.1元,甲种商品每天可多销售100件,商店决定把甲种商品的零售单价下降m(m>0)元,在不考虑其他因素的条件下,求当m为何值时,商店每天销售甲、乙两种商品获取的总利润为1800元(注:单件利润=零售单价﹣进货单价) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知OA=6,OB=10.点D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC﹣CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
(1)当点P经过点C时,求直线DP的函数解析式;
(2)①求△OPD的面积S关于t的函数解析式;
②如图②,把长方形沿着OP折叠,点B的对应点B′恰好落在AC边上,求点P的坐标.
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.



-
科目: 来源: 题型:
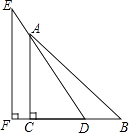
查看答案和解析>>【题目】一副直角三角板如图放置,点A在ED上,∠F=∠ACB=90°,∠E=30°,∠B=45°,AC=12,试求BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,斜坡AP的坡度为1:2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°.求:
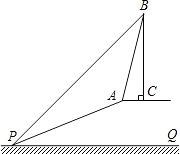
(1)坡顶A到地面PQ的距离;
(2)古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在6×8的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.

(1)以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′与△ABC位似,且位似比为1:2;(保留作图痕迹,不要求写作法和证明)
(2)若点C和坐标为(2,4),则点A′的坐标为( , ),点C′的坐标为( , ),S△A′B′C′:S△ABC= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BD、BE分别是△ABC的高线和角平分线,点F在CA的延长线上,FH⊥BE交BD于点G,交BC于点H.下列结论:①∠DBE=∠F;②∠BEF=
 (∠BAF+∠C); ③∠FGD=∠ABE+∠C;④∠F=
(∠BAF+∠C); ③∠FGD=∠ABE+∠C;④∠F= (∠BAC﹣∠C);其中正确的是_____.
(∠BAC﹣∠C);其中正确的是_____.
相关试题

