【题目】 如图1,在平面直角坐标系中,第一象限内长方形ABCD,AB∥y轴,点A是(1,1),点C(a,b),满足![]() .
.
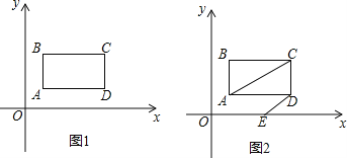
(1)求长方形ABCD的面积;
(2)如图2,长方形ABCD以每秒1个单位长度的速度向右平移,同时点E从原点O出发,沿x轴以每秒2个单位长度的速度向右运动,设运动时间为t秒.
①当t=5时,求三角形OMC的面积;
②若AC∥ED,求t的值.
参考答案:
【答案】(1)8;(2)①4;②3
【解析】
(1)由已知得出a=5,b=3,求得C点坐标,结合图象,能找出其它几点的坐标,从而能得出长方形ABCD的面积;
(2)①拆分三角形,求出各个图形的面积即可求得;
②过点A作AF∥CD,交x轴于点M,交DE的延长线于点F,根据平行四边形的性质可得出AF的长度,结合AM的长度可得出ME为△FAD的中位线,根据点M、A的运动速度可得出关于t的一元一次方程,解之即可得出结论.
解:(1)∵![]() .
.
∴a-5=0,b-3=0,即a=5,b=3,
∵四边形ABCD为长方形,
∴点B(1,3),点C(5,3),点D(5,1),
∴AB=3-1=2,BC=5-1=4,
长方形ABCD的面积为:AB×BC=2×4=8;
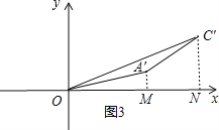
(2)①将t=5时,线段AC拿出来,放在图3中,各字母如图,
∵点A′(6,1),点C′(10,3),
∴OM=6,ON=10,A′M=1,C′N=3,MN=ON-OM=4,
∴三角形OA′C′的面积=![]() ONC′N-
ONC′N-![]() OMA′M-
OMA′M-![]() (A′M+C′N)MN=15-3-8=4;
(A′M+C′N)MN=15-3-8=4;
即三角形OMC的面积为4;
②过点A作AF∥CD,交x轴于点M,交DE的延长线于点F,
如图4所示,
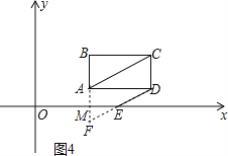
∵AF∥CD,AC∥DF,
∴四边形AFDC为平行四边形,
∴AF=CD=2.
∵AM=1,
∴ME为△FAD的中位线,
∴ME=![]() AD=2,
AD=2,
即2t-(t+1)=2,
解得:t=3.
故若AC∥ED,t的值为3秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=
 x-3与反比例函数y=
x-3与反比例函数y= 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.
(1)填空:n的值为 ,k的值为 ;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比函数y=
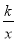 的图象,当y≥-2时,请直接写出自变量x的取值范围.
的图象,当y≥-2时,请直接写出自变量x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如:4=22-02,12=42-22,20=62-42,因此4,12,20都是“神秘数”.
(1)试分析28是否为“神秘数”;
(2)下面是两个同学演算后的发现,请选择一个“发现”,判断真、假,并说明理由.
①小能发现:两个连续偶数2k+2和2k(其中k取非负整数)构造的“神秘数”也是4的倍数.
②小仁发现:2016是“神秘数”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,点O是线段AD上一动点(不与点A、D重合),分别以AO和DO为边在AD的同侧作等边三角形OAB和等边三角形OCD,连结AC、BD相交于点E,连结OE.
(1)当点O为AD的中点时,求∠DEA的度数;
(2)在(1)的条件下,△ADE是轴对称图形吗?如果是,指出它的对称轴;如果不是,说明理由;
(3)当点O不在AD的中点时,求证EO平分∠DEA.


图① 图②
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知点D,E,F分别为BC,AD,AE的中点,且S△ABC=4cm2,则阴影部分面积S=( )cm2.
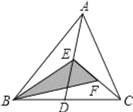
A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,
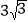 ),反比例函数
),反比例函数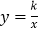 的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )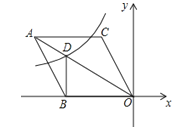
A.
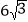 B. -
B. -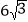 C.
C. 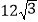 D. -
D. -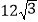
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AB=18,cosB=
 ,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E处,则线段AE的长为( )
,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E处,则线段AE的长为( )
A. 6
 B. 7
B. 7 C. 8
C. 8 D. 9
D. 9
相关试题

