【题目】如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如:4=22-02,12=42-22,20=62-42,因此4,12,20都是“神秘数”.
(1)试分析28是否为“神秘数”;
(2)下面是两个同学演算后的发现,请选择一个“发现”,判断真、假,并说明理由.
①小能发现:两个连续偶数2k+2和2k(其中k取非负整数)构造的“神秘数”也是4的倍数.
②小仁发现:2016是“神秘数”.
参考答案:
【答案】(1)28是“神秘数”(2)①是4的倍数,且是奇数倍②2016不是“神秘数”
【解析】
(1)根据题意设未知数x,列出对应方程x2-(x-2)2=28,求解即可.
(2)根据小能的发现列式:(2k+2)2-(2k)2化简,观察化简后的式子是否为4的倍数即可检验真假;根据小仁的发现列式:y2-(y-2)2=2 016求解,根据所得解即可检验真假.
(1)若28都是“神秘数”,设28是由x和x-2两数的平方差得到的
则x2-(x-2)2=28,解得:x=8,
∴x-2=6,
即28=82-62,28是“神秘数”
(2)① (2k+2)2-(2k)2=(2k+2-2k)(2k+2+2k)=4(2k+1),
∴由2k+2和2k构造的“神秘数”是4的倍数,且是奇数倍
或②设2 016是由y和y-2两数的平方差得到的,
则y2-(y-2)2=2 016,
解得:y=505,不是偶数,
∴2 016不是“神秘数”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,Rt△ABC中,∠C=90.
(1)当∠B=60时,
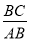 =_______;当∠A=45时,
=_______;当∠A=45时,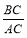 =_______.
=_______.(2)当∠B=2∠A时,求
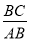 的值;
的值;(3)若AB=2BC,求∠A的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=
 x-3与反比例函数y=
x-3与反比例函数y= 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.
(1)填空:n的值为 ,k的值为 ;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比函数y=
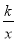 的图象,当y≥-2时,请直接写出自变量x的取值范围.
的图象,当y≥-2时,请直接写出自变量x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,点O是线段AD上一动点(不与点A、D重合),分别以AO和DO为边在AD的同侧作等边三角形OAB和等边三角形OCD,连结AC、BD相交于点E,连结OE.
(1)当点O为AD的中点时,求∠DEA的度数;
(2)在(1)的条件下,△ADE是轴对称图形吗?如果是,指出它的对称轴;如果不是,说明理由;
(3)当点O不在AD的中点时,求证EO平分∠DEA.


图① 图②
-
科目: 来源: 题型:
查看答案和解析>>【题目】 如图1,在平面直角坐标系中,第一象限内长方形ABCD,AB∥y轴,点A是(1,1),点C(a,b),满足
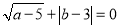 .
.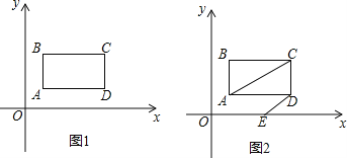
(1)求长方形ABCD的面积;
(2)如图2,长方形ABCD以每秒1个单位长度的速度向右平移,同时点E从原点O出发,沿x轴以每秒2个单位长度的速度向右运动,设运动时间为t秒.
①当t=5时,求三角形OMC的面积;
②若AC∥ED,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知点D,E,F分别为BC,AD,AE的中点,且S△ABC=4cm2,则阴影部分面积S=( )cm2.
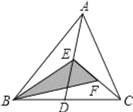
A. 1B. 2C. 3D. 4
相关试题

