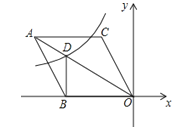
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,![]() ),反比例函数
),反比例函数![]() 的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
A. ![]() B. -
B. -![]() C.
C. ![]() D. -
D. -![]()
参考答案:
【答案】D
【解析】首先过点C 作CE⊥x 轴于点E,由∠BOC=60°,顶点C 的坐标为(m ,3![]() ),可求 得OC 的长,又由菱形ABOC 的顶点O 在坐标原点,边BO 在x 轴的负半轴上,可求 得OB 的长,且∠AOB=30°,继而求得DB 的长,则可求得点D 的坐标,又由反比例 函数
),可求 得OC 的长,又由菱形ABOC 的顶点O 在坐标原点,边BO 在x 轴的负半轴上,可求 得OB 的长,且∠AOB=30°,继而求得DB 的长,则可求得点D 的坐标,又由反比例 函数![]() 的图象与菱形对角线AO 交D 点,即可求得答案.
的图象与菱形对角线AO 交D 点,即可求得答案.
解:过点C 作CE⊥x 轴于点E,
∵顶点C 的坐标为(m ,3![]() ),
),
∴OE= ﹣m ,CE=3![]() ,
,
∵菱形ABOC 中,∠BOC=60°,
∴OB=OC=![]() =6 ,∠BOD=
=6 ,∠BOD=![]() ∠BOC=30°,
∠BOC=30°,
∵DB⊥x 轴,
∴DB=OBtan30°=6×![]() =2
=2![]() ,
,
∴点D 的坐标为:(﹣6,2![]() ),
),
∵反比例函数![]() 的图象与菱形对角线AO 交D 点,
的图象与菱形对角线AO 交D 点,
∴k=xy= ﹣12![]() .
.
故选D.
“点睛”此题考查了菱形的性质以及反比例函数图象上点的坐标特征.注意准确作出辅助线,
求得点D 的坐标是关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(0,3),C(1,0).
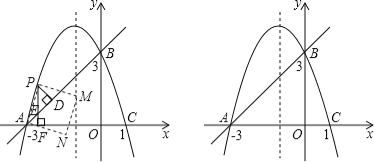
(1)求此抛物线的解析式.
(2)点P是直线AB上方的抛物线上一动点,(不与点A、B重合),过点P作x轴的垂线,垂足为F,交直线AB于点E,作PD⊥AB于点D.
①动点P在什么位置时,△PDE的周长最大,求出此时P点的坐标;
②连接PA,以AP为边作图示一侧的正方形APMN,随着点P的运动,正方形的大小、位置也随之改变.
当顶点M或N恰好落在抛物线对称轴上时,求出对应的P点的坐标.(结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面直角坐标系xOy中的图形W和点P,给出如下定义:F为图形W上任意一点,将P,F两点间距离的最小值记为m,最大值记为M,称M与m的差为点P到图形W的“差距离”,记作d(P,W),即d(P,W)=M-m,已知点A(2,1),B(-2,1)
(1)求d(O,AB);
(2)点C为直线y=1上的一个动点,当d(C,AB)=1时,点C的横坐标是 ;
(3)点D为函数y=x+b(-2≤x≤2)图象上的任意一点,当d(D,AB)≤2时,直接写出b的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品形状是长方体,长为8cm,它的展开图如图:
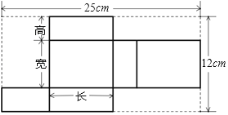
(1)求该长方体的宽和高;
(2)请为厂家设计一种包装纸箱,使每箱能装2件这种产品,要求没有空隙且要使该纸箱所用材料尽可能少(纸箱的表面积尽可能小),并求出该纸箱的体积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店购进一批甲、乙两种款型衬衫,甲种款型共用了7800元,乙种款型共用了6400元,甲种款型的件数是乙种款型件数的1.5倍,甲种款型每件的进价比乙种款型每件的进价少30元.
(1)求甲、乙两种款型的衬衫各购进多少件?
(2)商店进价提高60%标价销售,销售一段时间后,甲款型全部售完,乙款型剩余一半,商店决定对乙款型剩余的按标价的五折降价销售,很快全部售完。求售完这批衬衫商店共获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一船在灯塔
 的正东方向
的正东方向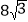 海里的
海里的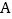 处,以20海里/时的速度沿北偏西
处,以20海里/时的速度沿北偏西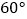 方向航行。
方向航行。(1)多长时间后,船距灯塔最近?
(2)多长时间后,船到灯塔的正北方向?此时船距灯塔有多远?
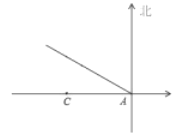
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图A在数轴上对应的数为-2.
(1)点B在点A右边距离A点4个单位长度,则点B所对应的数是_____.
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒3个单位长度沿数轴向右运动.现两点同时运动,当点A运动到-6的点处时,求A、B两点间的距离.
(3)在(2)的条件下,现A点静止不动,B点以原速沿数轴向左运动,经过多长时间A、B两点相距4个单位长度.

相关试题

