【题目】如图,已知∠AOB=α°,∠COD在∠AOB内部且∠COD=β°.
(1)若α,β满足|α-2β|+(β-60)2=0,则①α= ;
②试通过计算说明∠AOD与∠COB有何特殊关系;
(2)在(1)的条件下,如果作OE平分∠BOC,请求出∠AOC与∠DOE的数量关系;
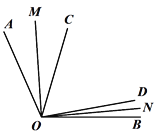
(3)若α°,β°互补,作∠AOC,∠DOB的平分线OM,ON,试判断OM与ON的位置关系,并说明理由.

参考答案:
【答案】(1)①α=120;②∠AOD与∠COB互补,理由见解析;(2)∠DOE=![]() ∠AOC,理由见解析;(3)OM⊥ON,理由见解析.
∠AOC,理由见解析;(3)OM⊥ON,理由见解析.
【解析】
(1)①根据非负数的性质即可得出结论;
②先表示出∠AOD=∠AOB-∠DOB=120°-∠DOB,∠COB=∠COB+∠DOB=60°+∠DOB,即可得到结论;
(2)根据角的和差以及角平分线的性质计算即可;
(3)根据角的和差、角平分线的性质以及互补的概念计算即可.
(1)①由题意得:α-2β=0,β=60°,解得:α=120°;
②∵∠AOB=α°=120°,∠COD=β°=60°,
∴∠AOD=∠AOB-∠DOB=120°-∠DOB,∠COB=∠COB+∠DOB=60°+∠DOB,∴∠AOD+∠COB=180°,即∠AOD与∠COB互补;
(2)设∠AOC=θ,则∠BOC=120°-θ.
∵OE平分∠BOC,∴∠COE=![]() ∠BOC=
∠BOC=![]() (120°-θ)=60°-
(120°-θ)=60°-![]() θ,
θ,
∴∠DOE=∠COD-∠COE=60°-60°+![]() θ=
θ=![]() θ=
θ=![]() ∠AOC;
∠AOC;
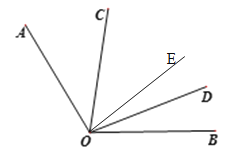
(3)OM⊥ON.理由如下:
∵OM,ON分别平分∠AOC,∠DOB,
∴∠COM=![]() ∠AOC,
∠AOC,
∴∠DON=![]() ∠BOD,
∠BOD,
∴∠MON=∠COM+∠COD+∠DON
=![]() ∠AOC+
∠AOC+![]() ∠BOD+∠COD
∠BOD+∠COD
=![]() (∠AOC+∠BOD)+∠COD
(∠AOC+∠BOD)+∠COD
=![]() (∠AOB-∠COD)+∠COD
(∠AOB-∠COD)+∠COD
=![]() (∠AOB+∠COD)
(∠AOB+∠COD)
=![]() (α°+β°)
(α°+β°)
∵α°,β°互补,
∴α°+β°=180°,
∴∠MON=90°,
∴OM⊥ON.
-
科目: 来源: 题型:
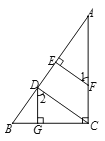
查看答案和解析>>【题目】如图所示,已知:DG⊥BC,AC⊥BC,FE⊥AB,∠1=∠2.
求证:CD⊥AB.
证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=∠ACB=90°(垂直的定义)
∴DG∥AC( )
∴∠2=∠DCA( )
∵∠1=∠2(已知)
∴∠1= (等量代换)
∴ (同位角相等,两直线平行)
∴ =∠ADC( )
∵EF⊥AB(已知), ∴∠AEF=90°( ),∴∠ADC=90° ,
∴CD⊥AB(垂直的定义)
-
科目: 来源: 题型:
查看答案和解析>>【题目】仔细阅读下列材料.
“分数均可化为有限小数或无限循环小数”,反之,“有限小数或无限小数均可化为分数”.
例如:
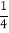 =1÷4=0.25;
=1÷4=0.25;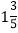 =
=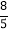 =8÷5=1.6;
=8÷5=1.6; =1÷3=
=1÷3= ,反之,0.25=
,反之,0.25=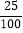 =
=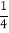 ;1.6=
;1.6=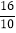 =
=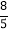 =
=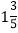 .那么
.那么 ,
,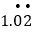 怎么化成分数呢?
怎么化成分数呢?解:∵
 ×10=3+
×10=3+ , ∴不妨设
, ∴不妨设 =x,则上式变为10x=3+x,解得x=
=x,则上式变为10x=3+x,解得x= ,即
,即 =
= ;
;∵
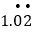 =
=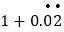 ,设
,设 =x,则上式变为100x=2+x,解得x=
=x,则上式变为100x=2+x,解得x=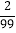 ,
,∴
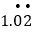 =
=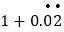 =1+x=1+
=1+x=1+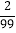 =
=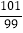
⑴将分数化为小数:
 =______,
=______,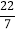 =_______;
=_______;⑵将小数化为分数:
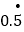 =______,
=______,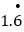 =_______;
=_______;⑶将小数
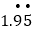 化为分数,需要写出推理过程.
化为分数,需要写出推理过程. -
科目: 来源: 题型:
查看答案和解析>>【题目】梧州市特产批发市场有龟苓膏粉批发,其中A品牌的批发价是每包20元,B品牌的批发价是每包25元,小王需购买A,B两种品牌的龟苓膏粉共1000包.
(1)若小王按需购买A,B两种品牌龟苓膏粉共用22000元,则各购买多少包?
(2)凭会员卡在此批发市场购买商品可以获得8折优惠,会员卡费用为500元.若小王购买会员卡并用此卡按需购买1000包龟苓膏粉,共用了y元,设A品牌买了x包,请求出y与x之间的函数关系式;
(3)在(2)中,小王共用了20000元,他计划在网店包邮销售这批龟苓膏粉,每包龟苓膏粉小王需支付邮费8元,若每包销售价格A品牌比B品牌少5元,请你帮他计算,A品牌的龟苓膏粉每包定价不低于多少元时才不亏本?(运算结果取整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=50°,BC=6,以BC为直径的半圆O与AB、AC分别交于点D、E,则图中阴影部分面积之和等于(结果保留π).
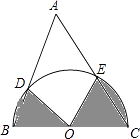
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,MN为⊙O的直径,A、B是⊙O上的两点,过A作AC⊥MN于点C,过B作BD⊥MN于点D,P为DC上的任意一点,若MN=20,AC=8,BD=6,则PA+PB的最小值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】新农村社区改造中,有一部分楼盘要对外销售,某楼盘共23层,销售价格如下:第八层楼房售价为4000元/米2,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,已知该楼盘每套楼房面积均为120米2.
若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价8%,另外每套楼房赠送a元装修基金;
方案二:降价10%,没有其他赠送.
(1)请写出售价y(元/米2)与楼层x(1≤x≤23,x取整数)之间的函数关系式;
(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
相关试题

