【题目】回答下列问题:
(1)如图所示的甲、乙两个平面图形能折什么几何体?
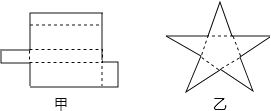
(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点个数为v,棱数为e,分别计算第(1)题中两个多面体的f+v﹣e的值?你发现什么规律?
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
参考答案:
【答案】(1)甲是长方体,乙是五棱锥;(2)甲:![]() =2,乙:
=2,乙:![]() =2,规律:顶点数+面数-棱数=2;(3)22.
=2,规律:顶点数+面数-棱数=2;(3)22.
【解析】(1)根据平面图形的展开图的特征即可作出判断;
(2)分别数出甲、乙两个平面图形围成的几何体的面数、顶点个数、棱数,即可得到规律;
(3)设这个多面体的面数为![]() ,根据(2)中得到的规律即可列方程求解.
,根据(2)中得到的规律即可列方程求解.
解:(1)甲是长方体,乙是五棱锥;
(2)甲:f=6,e=12,v=8,f+v–e=2
乙:f=6,e=10,v=6,f+v–e=2
规律:顶点数+面数-棱数=2;
(3)设这个多面体的面数为![]() ,由题意得
,由题意得![]() +
+ ![]() +8-50=2,解得
+8-50=2,解得![]() =22
=22
答:这个几何体的面数为22.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:点P为△ABC内部或边上的点,若满足△PAB,△PBC,△PAC至少有一个三角形与△ABC相似(点P不与△ABC顶点重合),则称点P为△ABC的自相似点.

例如:如图1,点P在△ABC的内部,∠PBC=∠A,∠PCB=∠ABC,则△BCP∽△ABC,故点P为△ABC的自相似点.
在平面直角坐标系xOy中,
(1)点A坐标为(
 ,
,  ), AB⊥x轴于B点,在E(2,1),F (
), AB⊥x轴于B点,在E(2,1),F ( ,
,  ),G (
),G ( ,
,  ),这三个点中,其中是△AOB的自相似点的是 (填字母);
),这三个点中,其中是△AOB的自相似点的是 (填字母);(2)若点M是曲线C:
 (
( ,
,  )上的一个动点,N为x轴正半轴上一个动点;
)上的一个动点,N为x轴正半轴上一个动点; 图2
图2① 如图2,
 ,M点横坐标为3,且NM = NO,若点P是△MON的自相似点,求点P的坐标;
,M点横坐标为3,且NM = NO,若点P是△MON的自相似点,求点P的坐标;②若
 ,点N为(2,0),且△MON的自相似点有2个,则曲线C上满足这样条件的点M共有 个,请在图3中画出这些点(保留必要的画图痕迹).
,点N为(2,0),且△MON的自相似点有2个,则曲线C上满足这样条件的点M共有 个,请在图3中画出这些点(保留必要的画图痕迹).
-
科目: 来源: 题型:
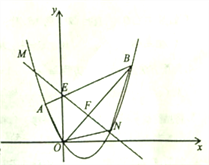
查看答案和解析>>【题目】(12分)如图,平面直角坐标系
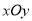 中点
中点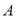 的坐标为
的坐标为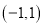 ,点
,点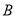 的坐标为
的坐标为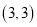 ,抛物线经过
,抛物线经过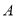 、
、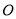 、
、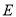 三点,连接
三点,连接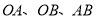 ,线段
,线段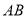 交
交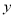 轴于点
轴于点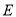 .
.
(1)求点
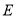 的坐标;
的坐标;(2)求抛物线的函数解析式;
(3)点
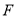 为线段
为线段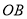 上的一个动点(不与点
上的一个动点(不与点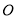 、
、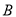 重合),直线
重合),直线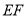 与抛物线交于
与抛物线交于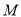 、
、 两点(点
两点(点 在
在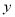 轴右侧),连接
轴右侧),连接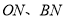 ,当四边形
,当四边形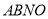 的面积最大时,求点
的面积最大时,求点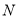 的坐标并求出四边形
的坐标并求出四边形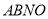 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知12箱苹果,以每箱10千克为标准,超过10千克的数记为正数,不足10千克的数记为负数,称重记录如下:
+0.2 ,—0.2,+0. 7,—0.3,—0.4,+0.6,0,—0.1,—0.6,+0.5,—0.2,—0.5。
⑴求12箱苹果的总重量;
⑵若每箱苹果的重量标准为10
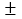 0.5(千克),则这12箱有几箱不合乎标准的?
0.5(千克),则这12箱有几箱不合乎标准的? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣(k+1)x+2k﹣2=0.
(1)求证:此方程总有两个实数根;
(2)若此方程有一个根大于0且小于1,求k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某小区的一个健身器材,已知BC=0.15m,AB=2.70m,∠BOD=70°,求端点A到地面CD的距离(精确到0.1m).(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,
(1)写出数轴上点B表示的数 ;
(2)|5﹣3|表示5与3之差的绝对值,实际上也可理解为5与3两数在数轴上所对的两点之间的距离.如|x﹣3|的几何意义是数轴上表示有理数x的点与表示有理数3的点之间的距离.试探索:
①:若|x﹣8|=2,则x= .
②:|x+12|+|x﹣8|的最小值为 .
(3)动点P从O点出发,以每秒5个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.求当t为多少秒时?A,P两点之间的距离为2;
(4)动点P,Q分别从O,B两点,同时出发,点P以每秒5个单位长度沿数轴向右匀速运动,Q点以P点速度的两倍,沿数轴向右匀速运动,设运动时间为t(t>0)秒.问当t为多少秒时?P,Q之间的距离为4.
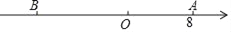
相关试题

