【题目】已知关于x的一元二次方程x2﹣(k+1)x+2k﹣2=0.
(1)求证:此方程总有两个实数根;
(2)若此方程有一个根大于0且小于1,求k的取值范围.
参考答案:
【答案】(1)证明见解析;(2)1<k<2.
【解析】
(1)根据方程的系数结合根的判别式,求得判别式![]() 恒成立,因此得证;
恒成立,因此得证;
(2)利用求根公式求根,根据有一个跟大于0且小于1,列出关于![]() 的不等式组,解之即可.
的不等式组,解之即可.
(1)证明:△=b2-4ac=[-(k+1)]2-4×(2k-2)=k2-6k+9=(k-3)2,
∵(k-3)2≥0,即△≥0,
∴此方程总有两个实数根,
![]()
解得x1=k-1,x2=2,
∵此方程有一个根大于0且小于1,
而x2>1,
∴0<x1<1,
即0<k-1<1.
∴1<k<2,
即k的取值范围为:1<k<2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形纸片ABC的面积为48,BC的长为8.按下列步骤将三角形纸片ABC进行裁剪和拼图:
第一步:如图1,沿三角形ABC的中位线DE将纸片剪成两部分.在线段DE上任意取一点F,在线段BC上任意取一点H,沿FH将四边形纸片DBCE剪成两部分;
第二步:如图2,将FH左侧纸片绕点D旋转180°,使线段DB与DA重合;将FH右侧纸片绕点E旋转180°,使线段EC与EA重合,再与三角形纸片ADE拼成一个与三角形纸片ABC面积相等的四边形纸片.


图1 图2
(1)当点F,H在如图2所示的位置时,请按照第二步的要求,在图2中补全拼接成的四边形;
(2)在按以上步骤拼成的所有四边形纸片中,其周长的最小值为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=
 x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点. 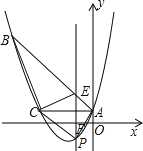
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对角线AC,BD相交于点O,将BD向两个方向延长,分别至点E和点F,且使BE=DF.
(1)求证:四边形AECF是菱形;
(2)若AC=4,BE=1,直接写出菱形AECF的边长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一次数学测试后,随机抽取6名学生成绩如下:86,85,88,80,88,95,关于这组数据说法错误的是( )
A.方差是20
B.众数是88
C.中位数是86
D.平均数是87 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,内部有6个全等的正方形,小正方形的顶点E、F、G、H分
别在边AD、AB、BC、CD上,则tan∠DEH=( )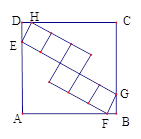
A.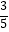
B.
C.
D.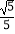
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线经过A(1,0),B(4,0),C(0,-4)三点,点D是直线BC上方的抛物线上的一个动点,连结DC,DB,则△BCD的面积的最大值是( )
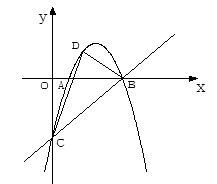
A.7
B.7.5
C.8
D.9
相关试题

