【题目】如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证: 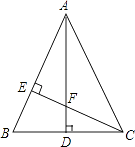
(1)△AEF≌△CEB;
(2)AF=2CD.
参考答案:
【答案】
(1)证明:∵AD⊥BC,CE⊥AB,
∴∠BCE+∠CFD=90°,∠BCE+∠B=90°,
∴∠CFD=∠B,
∵∠CFD=∠AFE,
∴∠AFE=∠B
在△AEF与△CEB中,
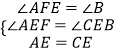 ,
,
∴△AEF≌△CEB(AAS)
(2)证明:∵AB=AC,AD⊥BC,
∴BC=2CD,
∵△AEF≌△CEB,
∴AF=BC,
∴AF=2CD
【解析】(1)由AD⊥BC,CE⊥AB,易得∠AFE=∠B,利用全等三角形的判定得△AEF≌△CEB;(2)由全等三角形的性质得AF=BC,由等腰三角形的性质“三线合一”得BC=2CD,等量代换得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有两块面积相同的试验田,分别收获蔬菜900kg和1500kg,已知第一块试验田每亩收获蔬菜比第二块少300kg,求第一块试验田每亩收获蔬菜多少千克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据题意解答
(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得线段BE、EF、FD之间的数量关系为 .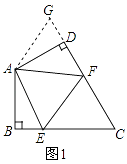
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且∠EAF= ∠BAD,线段BE、EF、FD之间存在什么数量关系,为什么?
∠BAD,线段BE、EF、FD之间存在什么数量关系,为什么?
(3)如图3,点A在点O的北偏西30°处,点B在点O的南偏东70°处,且AO=BO,点A沿正东方向移动249米到达E处,点B沿北偏东50°方向移动334米到达点F处,从点O观测到E、F之间的夹角为70°,根据(2)的结论求E、F之间的距离.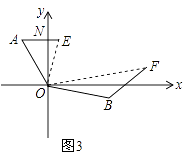
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的三个顶点的坐标分别为:A(﹣2,3)、B(﹣6,0)、C(﹣1,0).

(1)将△ABC沿y轴翻折,画出翻折后的△A1B1C1 , 点A的对应点A1的坐标是
(2)△ABC关于x轴对称的图形△A2B2C2 , 直接写出点A2的坐标
(3)若△DBC与△ABC全等(点D与点A重合除外),请直接写出满足条件点D的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】有两块面积相同的试验田,分别收获蔬菜900kg和1500kg,已知第一块试验田每亩收获蔬菜比第二块少300kg,求第一块试验田每亩收获蔬菜多少千克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,正比例函数y=x的图象与一次函数y=kx﹣k的图象的交点坐标为A(m,2).
(1)求m的值和一次函数的解析式;
(2)设一次函数y=kx﹣k的图象与y轴交于点B,求△AOB的面积;
(3)直接写出使函数y=kx﹣k的值大于函数y=x的值的自变量x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某人沿一条直路行走,此人离出发地的距离
 千米
千米 与行走时间
与行走时间 分钟
分钟 的函数关系如图所示,请根据图象提供的信息回答下列问题:
的函数关系如图所示,请根据图象提供的信息回答下列问题: 此人离开出发地最远距离是______ 千米;
此人离开出发地最远距离是______ 千米; 此人在这次行走过程中,停留所用的时间为______ 分钟;
此人在这次行走过程中,停留所用的时间为______ 分钟; 由图中线段OA可知,此人在这段时间内行走的速度是每小时______ 千米;
由图中线段OA可知,此人在这段时间内行走的速度是每小时______ 千米; 此人在120分钟内共走了______ 千米.
此人在120分钟内共走了______ 千米.
相关试题

