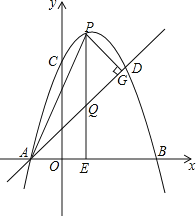
【题目】如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),C(0,3)两点,点B是抛物线与x轴的另一个交点,点D与点C关于抛物线对称轴对称,作直线AD.点P在抛物线上,过点P作PE⊥x轴,垂足为点E,交直线AD于点Q,过点P作PG⊥AD,垂足为点G,连接AP.设点P的横坐标为m,PQ的长度为d.
(1)求抛物线的解析式;
(2)求点D的坐标及直线AD的解析式;
(3)当点P在直线AD上方时,求d关于m的函数关系式,并求出d的最大值;
(4)当点P在直线AD上方时,若PQ将△APG分成面积相等的两部分,直接写出m的值.
参考答案:
【答案】(1)y=﹣x2+2x+3;(2)点D的坐标为(2,3),直线AD的解析式为y=x+1;(3)d关于m函数关系式是d=﹣m2+m+2,d的最大值为![]() ;(4)m的值为0
;(4)m的值为0
【解析】
(1)根据待定系数法可求抛物线的解析式;
(2)将y=﹣x2+2x+3配方得抛物线的对称轴,根据轴对称的性质可得点D的坐标,再根据待定系数法可求直线AD的解析式;
(3)根据两点间的距离公式可得d=﹣m2+2m+3﹣m﹣1=﹣m2+m+2=﹣(m﹣![]() )2+
)2+![]() ,依此可求d的最大值;
,依此可求d的最大值;
(4)可设直线PG的解析式为y=﹣x+p,根据中点坐标公式可得G的坐标,再根据待定系数法可求m的值.
解:(1)∵抛物线y=﹣x2+bx+c 经过A(﹣1,0),C(0,3)两点,
∴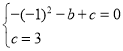 ,
,
解得![]() .
.
∴抛物线的解析式为y=﹣x2+2x+3.
(2)∵将y=﹣x2+2x+3配方,得y=﹣(x﹣1)2+4,
∴抛物线的对称轴是直线x=1.
∴点D的坐标为(2,3).
设直线AD的解析式为y=kx+n,
由题意,得![]() ,
,
解得![]() .
.
∴直线AD的解析式为y=x+1.
(3)∵点P的横坐标为m,
∴点P,Q的纵坐标分别为﹣m2+2m+3,m+1,
∴d=﹣m2+2m+3﹣m﹣1=﹣m2+m+2=![]() ,
,
∴d关于m函数关系式是d=﹣m2+m+2,d的最大值为![]() .
.
(4)设直线PG的解析式为y=﹣x+p,
∵PQ将△APG分成面积相等的两部分,
∴G的坐标为(2m+1,2m+2),
∴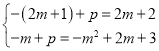 ,
,
解得m1=0,m2=﹣1(不合题意舍去).
故m的值为0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年春节期间,兰州市开展了以“精致兰州志愿同行”为主题的系列志愿服务活动.金老师和程老师积极参加志愿者活动,当时有下列四个志愿者工作岗位供他们选择:
①“送温暖”活动岗位:为困难家庭打扫卫生,为留守儿童提供学业辅导;(分别用
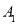 ,
,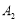 表示)
表示)②“送平安”活动岗位:消防安全常识宣传,人员密集场所维护秩序.(分别用
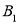 ,
,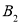 表示)
表示)(1)金老师从四个岗位中随机选取一个报名,恰好选择“送温暖”活动岗位的概率是多少?
(2)若金老师和程老师各随机从四个活动岗位中选一个报名,请用树状图或列表法求出他们恰好都选择同一个岗位的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,池塘边一棵垂直于水面BM的笔直大树AB在点C处折断,AC部分倒下,点A与水面上的点E重合,部分沉入水中后,点A与水中的点F重合,CF交水面于点D,DF=2m,∠CEB=30°,∠CDB=45°,求CB部分的高度.(精确到0.1m.参考数据:
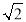 ≈1.41,
≈1.41,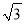 ≈1.73)
≈1.73)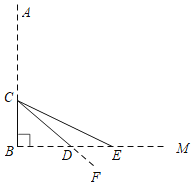
-
科目: 来源: 题型:
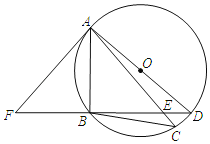
查看答案和解析>>【题目】如图,AD是⊙O的直径,弧BA=弧BC,BD交AC于点E,点F在DB的延长线上,且∠BAF=∠C.
(1)求证:AF是⊙O的切线;
(2)求证:△ABE∽△DBA;
(3)若BD=8,BE=6,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学分别进行6次射击训练,训练成绩(单位:环)如下表
第一次
第二次
第三次
第四次
第五次
第六交
甲
9
8
6
7
8
10
乙
8
7
9
7
8
8
对他们的训练成绩作如下分析,其中说法正确的是( )
A. 他们训练成绩的平均数相同 B. 他们训练成绩的中位数不同
C. 他们训练成绩的众数不同 D. 他们训练成绩的方差不同
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AC≤BC,将△ABC沿EF折叠,使点A落在直角边BC上的D点处,设EF与AB、AC边分别交于点E、点F,如果折叠后△CDF与△BDE均为等腰三角形,那么∠B=_____.
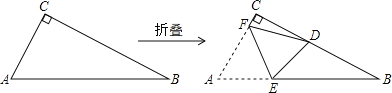
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校有
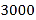 名学生,为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
名学生,为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.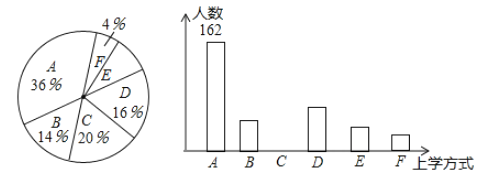
根据以上信息,回答下列问题:
(1)参与本次问卷调查的学生共有_____人,其中选择
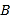 类的人数有_____人;
类的人数有_____人;(2)在扇形统计图中,求
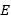 类对应的扇形圆心角
类对应的扇形圆心角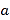 的度数,并补全条形统计图;
的度数,并补全条形统计图;(3)若将
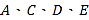 这四类上学方式视为“绿色出行”,请估计该校选择“绿色出行”的学生人数.
这四类上学方式视为“绿色出行”,请估计该校选择“绿色出行”的学生人数.
相关试题

